Sau khi phát triển được một mô hình (model) đạt được độ chính xác theo yêu cầu. Việc tiếp theo có lẽ chúng ta sẽ phải làm trước khi triển khai mô hình là tối ưu về tốc độ(speed), bộ nhớ(memory footprint) và năng lượng(energy). Những cách phổ biến có thể nghĩ đến là lượng tử hóa(quantization), chưng cất hiểu biết(knowledge distillation) và cắt tỉa trọng số(weight pruning). Trong bài này, chúng ta sẽ cùng bàn luận về bài báo(paper) như tiêu đề, bài báo về chủ đề cắt tỉa trọng số của mô hình. Bài viết này đã xuất bản được hơn 2 năm và làm cơ sở cho nhiều bài báo sau này. Tuy gần đây cũng có bài báo chỉ ra sự không hiệu quả của phương pháp trong bài báo này, song việc tìm hiểu cả hai chiều giúp chúng ta có được cái nhìn mới về những khía cạnh xung quanh việc huấn luyện mô hình.
Giới thiệu

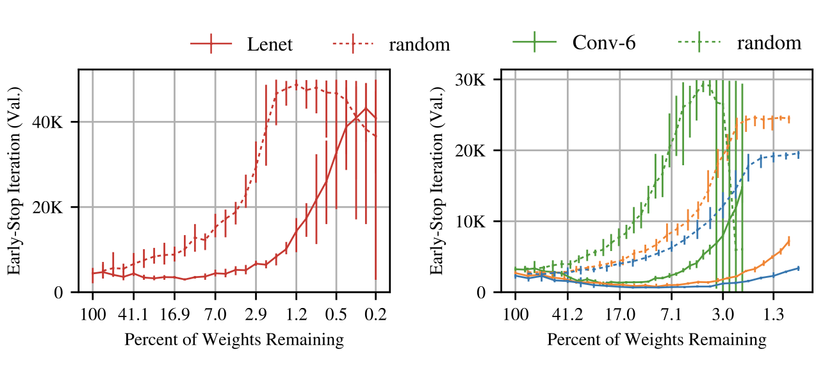

Trong paper này, tác giả chỉ ra rằng luôn tồn tại một mạng con(subnetwork) nhỏ hơn mà nếu huấn luyện chúng từ đầu và học trong thời gian nhiều nhất là bằng với mô hình gốc thì sẽ đạt tới độ chính xác(accuracy) tương tự mạng gốc. Đường nét liền trong hình trên thể hiện mạng tác giả tìm được theo phương pháp trong bài báo (winning ticket, trung bình 5 lần thử). Đường nét đứt là các mạng thưa được lấy mẫu ngẫu nhiên(trung bình 10 lần thử)
Định nghĩa
Giả thuyết vé số (The Lottery Ticket Hypothesis): một mạng nơ-ron đặc (dense neural network) khởi tạo một cách ngẫu nhiên sẽ chứa một mạng con (subnetwork), mạng con đó khi được huấn cô lập có thể thu được độ chính xác tương tự với mạng gốc sau khi huấn luyện với cùng số lần lặp(iteration) với mô hình gốc, hoặc có thể ít hơn.
Cụ thể, xét một mạng nơ rơn đặc với tham số khởi tạo . Khi tối ưu với stochastic gradient descent(SGD) trên một tập training set, đạt validation loss cực tiểu tại lần lặp với độ chính xác là . Thêm vào đó, xét việc huấn luyện ) với mặt nạ của tham số để khởi tạo của nó trở thành . Khi tối ưu với SGD trên cùng một tập training (với cố định), đạt validation loss cực tiểu tại lần lặp với độ chính xác . Giả thuyết vé số dự đoán rằng thỏa mãn (tương đương về mặt thời gian huấn luyện), (tương đương về độ chính xác), và (số tham số ít hơn).
Tác giả cho rằng các phương pháp cắt tỉa tiêu chuẩn tự động để tiết lộ một mạng con như vậy từ mạng fully-connected và convolutional. Mạng này được gọi là vé thắng(winning ticket). Vé thắng này là tổ hợp của vị trí các kết nối (connection) và các trọng số khởi tạo ban đầu của chúng hay . Nếu chúng ta sử dụng các connection này với các trọng số được khởi tạo lại trong đó , vé này sẽ không còn là vé thắng vì nó không cho performance tốt như mô hình gốc.
Tìm vé thắng
Chúng ta tìm vé thắng bằng cách huấn luyện một mạng và tỉa những trọng số có độ lớn nhỏ nhất. Phần còn lại là những kết nối tạo lên kiến trúc của vé thắng. Giá trị của các kết nối không bị tỉa được reset trở về giá trị ban đầu của chúng trước khi huấn luyện. Các bước để tìm vé thắng:
- Khởi tạo ngẫu nhiên một mạng nơ ron trong đó .
- Huấn luyện mạng trong lần lặp, thu được .
- Tỉa số tham số của , tạo mặt nạ .
- Reset những tham số còn lại về giá trị ban đầu của chúng trong , tạo thành vé thắng
Bốn bước trên tương ứng với phương pháp tỉa one-shot. Tuy nhiên, trong bài báo, tác giả tập trung vào tỉa lặp lại (iterative pruning), nghĩa là lặp lại việc huấn luyện, tỉa, và reset mô hình vòng(round), mỗi lần tỉa số trọng số còn lại từ vòng trước.
Kết quả
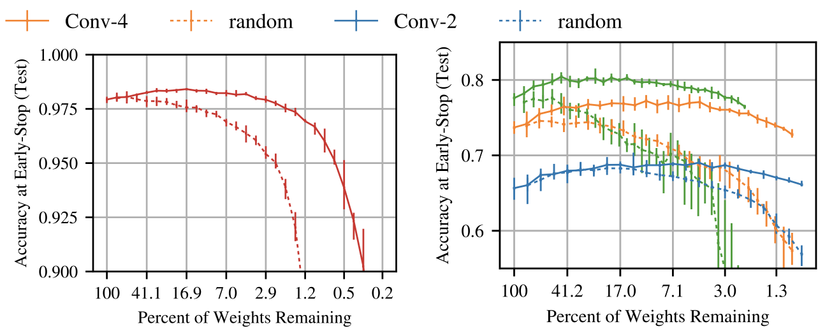
Tác giả tìm vé thắng trong kiến trúc fully-connected cho MNIST và kiến trúc tích chập cho CIFAR10 cùng với vài chiến lược tối ưu (SGD, momentum và Adam) với các kỹ thuật như dropout, weight decay, batchnorm và residual connection. Tác giả sử dụng kỹ thuật tỉa không cấu trúc (unstructured pruning). Với các mạng sâu hơn, chiến lược dựa vào cắt tỉa để tìm ra vé thắng nhạy cảm với tốc độ học (leanring rate): nó yêu cầu warmup để tìm tìm vé thắng ở learning rate cao hơn. Vé thắng tác giả tìm thấy chỉ chiếm 10-20% kích thước của mạng gốc nhưng vẫn đạt hoặc vượt độ chính xác của mạng gốc. Khi khởi tạo lại ngẫu nhiên, vé thắng cho kết quả tệ hơn, điều này có nghĩa là chỉ riêng cấu trúc mạng sẽ không đủ để tạo nên thành công của vé thắng.
Vé thắng trong mạng fully-connected

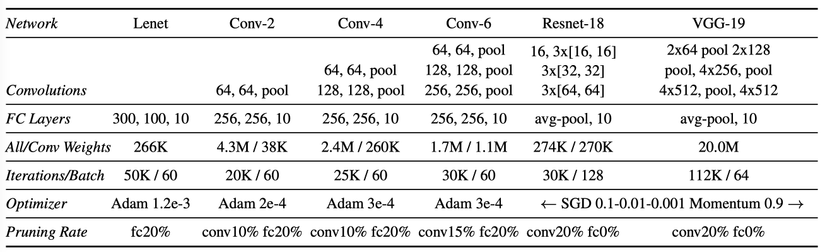
Tác giả đánh giá giả thuyết vé số với mạng fully-connected được huấn luyện trên tập MNIST. Mô hình được sử dụng là Lenet-300-100 mô tả ở hình trên. Các bước được tiến hành như ở phần giới thiệu: sau khi khởi tạo ngẫu nhiên và huấn luyện mạng, tác giả tỉa mạng và reset các kết nối còn lại về giá trị khởi tạo. Việc cắt tỉa được thực hiện bằng cách loại bỏ theo phần trăm các trọng số có độ lớn nhỏ nhất của mỗi lớp(layer). Các kết nối với đầu ra(outputs) được tỉa bằng một nửa tỷ lệ của phần còn lại của mạng.
Định nghĩa là độ thưa của mặt nạ . Ví dụ, khi 75% trọng số được tỉa.

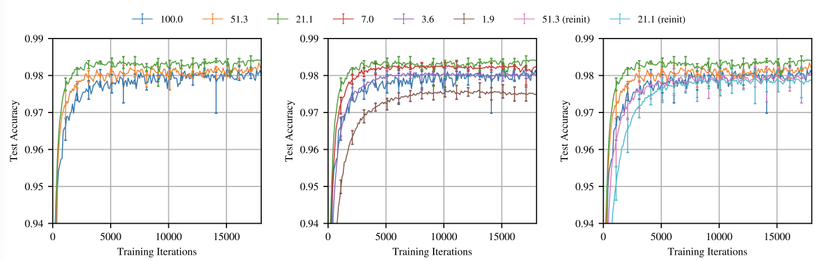
Tỉa lặp lại (iterative pruning). Vé thắng chúng ta tìm học nhanh hơn mạng gốc. Hình trên thể hiện độ chính xác trung bình khi huấn luyện vé số theo cách lặp lại với nhiều mức độ. Trong vòng tỉa đầu tiên, mạng học nhanh hơn và đạt độ chính xác cao hơn là những mạng được tỉa nhiều hơn(trong hình bên trái). Vé thắng gồm 51.3% trọng số từ mạng gốc() đạt độ chính xác cao hơn và nhanh hơn mạng gốc nhưng chậm hơn so với . Khi , quá trình học bắt đầu chậm hơn(hình ở giữa). Khi , vé thắng có performance thấp hơn so với mạng gốc. Một pattern tương tự lặp lại trong các thử nghiệm trong suốt bài báo.
Khởi tạo lại ngẫu nhiên (Random reinitialization): để đo sự quan trọng của việc khởi tạo của vé thắng, tác giả giữ lại cấu trúc của vé thắng nhưng khởi tạo mới . Tác giả thấy rằng khởi tạo là yếu tố quyết định cho sự hiệu quả của vé thắng. Mô hình học chậm hơn và cho độ chính xác thấp hơn khi khởi tạo lại ngẫu nhiên.
One-shot pruning: mặc dù việc tỉa lặp lại trích xuất vé thắng nhỏ hơn, nhưng việc lặp lại khiến chúng sẽ tốn chi phí để tìm. Tỉa one-shot là phương pháp khả thi để tìm vé thắng mà không phải lặp lại quá trình huấn luyện. Vé thắng được tỉa một cách lặp lại sẽ học nhanh hơn và đạt được độ chính xác cao hơn với kích thước mạng nhỏ hơn.
Vé thắng trong mạng tích chập
Tác giả thử nghiệm trên CIFAR10, tăng cả độ phức tạp của bài toán và kích thước của mạng. Xét các kiến trúc Conv-2, Conv-4, Conv-6, là các biến thể nhỏ hơn của họ VGG. Các mạng này có 2, 4, 6 lớp tích chập theo sau là hai lớp fully-connected; max-pooling sau mỗi hai lớp tích chập.

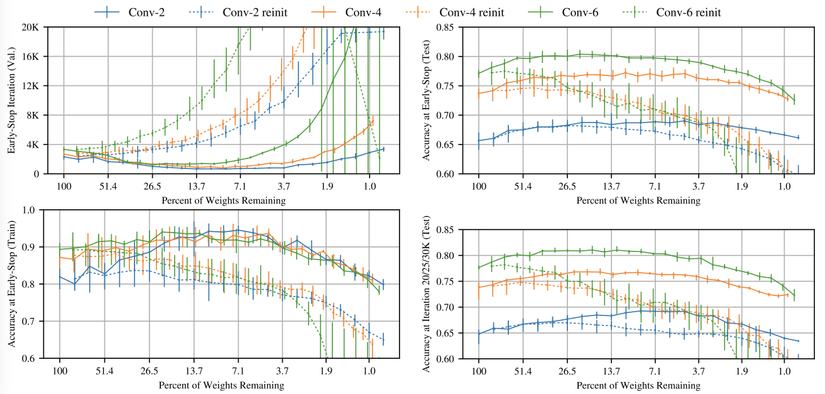
Tìm vé thắng: đường nét liền trong hình trên thể hiện thí nghiệm vé số lặp lại trên Conv-2(blue), Conv-4(orange), và Conv-6 ở tỷ lệ tỉa theo từng lớp. Pattern từ Lenet trong phần trước lặp lại: khi mạng được tỉa, nó học nhanh hơn và độ chính xác tăng so với mạng gốc. Trong trường hợp này, kết quả khá dễ thấy. Vé thắng đạt validation loss cực tiểu và nhanh hơn 3.5 lần với Conv-2 (), 3.5 lần với Conv-4(), và 2.5 lần với Conv-6(). Cả ba mạng đều cho độ chính xác cao hơn độ chính xác trung bình gốc khi
Global pruning. Trong Lenet và Conv-2/4/6, tác giả tỉa mỗi lớp riêng biệt với cùng tỷ lệ. Với Resnet-18 và VGG-19, tác giả sử dụng tỉa toàn cục(global pruning), loại bỏ những trọng số có độ lớn thấp nhất trong tất cả các lớp tích chập. Tác giả phỏng đoán rằng với những mạng sâu hơn, có những lớp sẽ có nhiều tham số hơn các lớp khác. Ví dụ như, hai lớp tích chập đầu tiên của VGG có 1728 và 36864 tham số trong khi đó 2 lớp cuối có 2.35 triệu. Khi tất cả các lớp được tỉa với cùng tỷ lệ, những lớp nhỏ hơn này trở thành nút thắt cổ chai.
Những điểm hạn chế
Trong bài báo tác giả chỉ xét những dataset nhỏ như MNIST và CIFAR10 và cần có phương pháp hiệu quả hơn để tìm vé thắng với những bài toán phức tạp hơn, có dataset lớn hơn như ImageNet.
Với những mạng sâu hơn (Resnet-18 và VGG-19), tỉa lặp lại không thể tìm thấy vé thắng trừ khi huấn luyện với tốc độ học khởi động (learning rate warmup). Do đó khi sử dụng learning rate thường được áp dụng cho các mạng này thì không thể sử dụng phương pháp này để tìm vé thắng.
Lời kết
Trong bài này, mình đã tóm tắt các ý chính trong bài báo. Cá nhân mình thấy phương pháp này chỉ có ứng dụng với những mạng nhỏ, nhưng kết quả của bài báo này là khá bất ngờ và rất nhiều bài báo sau này đã dựa trên khám phá này. Cũng có một bài báo mới đây đã chỉ ra điều kiện để tìm ra winning ticket và kết luận rằng phương pháp này không hiệu quả với những model cần huấn luyện với leanring rate lớn. Tuy vậy, mình đánh giá bài báo này đã có những khám phá mới giúp chúng ta có những hướng đi mới trong việc pruning model và hiểu hơn về các yếu tố xung quanh việc huấn luyện mạng.