Xin chào tất cả các bạn, hôm nay chung ta lại cùng nhau trở lại với một bài viết phân tích paper nhé. Khác với những bài viết trước chúng ta thường tiến hành phân tích những kiến trúc mạng mới thì hôm nay chúng ta sẽ cùng nhau tìm hiểu một phương pháp data augmentation khá đơn giản nhưng lại hiệu quả trong các bài toán image classification. Phương pháp này có tên là mixup augmentation được giới thiệu trong paper mixup: BEYOND EMPIRICAL RISK MINIMIZATION nằm trong hội thảo ICLR 2018 bởi nhóm nghiên cứu của các nhà khoa học thuộc MIT và Facebook Research. OK chúng ta sẽ bắt đầu ngay thôi

Lời mở đầu

Image classification - bài toán phân loại hình ảnh là một trong những bài toán đã quá nổi tiếng đối với các bạn làm trong lĩnh vực AI này. Có lẽ chúng ta không cần phải tốn quá nhiều giấy mực để nói lại về nó nữa. Với bất kì ai tiếp cận với Deep Learning đều không còn xa lạ gì với các model được training từ tập ImageNet - một challenge nổi tiếng trong phân loại hình ảnh. Để tiếp cận bài toán này người ta có hai hướng tiếp cận.

Các phương pháp xử lý ảnh truyền thống để tiếp cận cho bài toán này tiến hành các phương pháp xử lý trực tiếp trên ảnh đầu vào như dilations/erosions, sử dụng kernel hay chuyển ảnh về miền tần số và tiến hành chọn lựa các đặc trưng trên đó. các phương pháp xử lý ảnh truyền thống thực hiện rất thủ công và thường không hiệu quả đối với các large-scale dataset.

Cách tiếp cận của học sâu mặt khác tập trung vào việc tìm các mối tương quan giữa ảnh đầu vào và label của nó thông qua việc tuning các kiến trúc mạng nơ ron phức tạp. Tuy nhiên việc huấn luyện một mạng nơ ron thường đòi hỏi một số lượng dữ liệu rất lớn và đa dạng. Chính vì thế mà các phương pháp để tăng cường dữ liệu được tập trung nghiên cứu. Paper hôm nay chúng ta tìm hiểu là một trong những nghiên cứu như vậy.

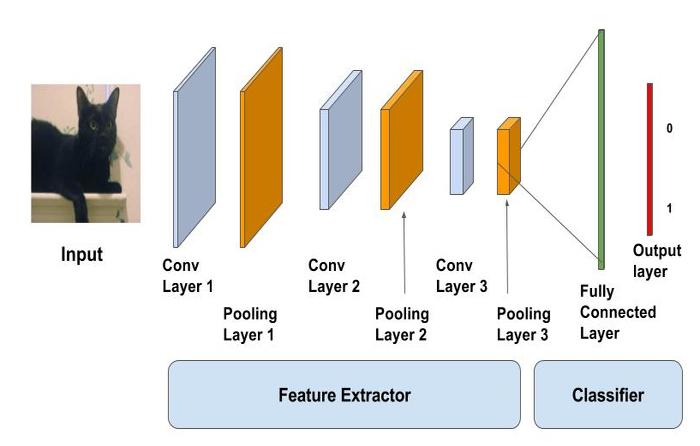
Các khái niệm chính liên quan

Data Augmentation

Mục đích cuối cùng của việc huấn luyện một mô hình Machine Learning nói chúng đó chính là việc có thể đưa ra dược những dự đoán dáng tin cậy cho những mẫu dữ liệu mới mà mô hình chưa từng nhìn thấy bao giờ. Khái niệm này được gọi là tổng quát hoá - generalize tốt cho dữ liệu mới. Để làm được điều đó người ta thường hạn chế tối đa việc để các mô hình của ình rơi vào một trong các trạng thái over-fiting, under-fitting. Đây là những concept rất cơ bản của học máy mình sẽ không đề cập sâu ở đây

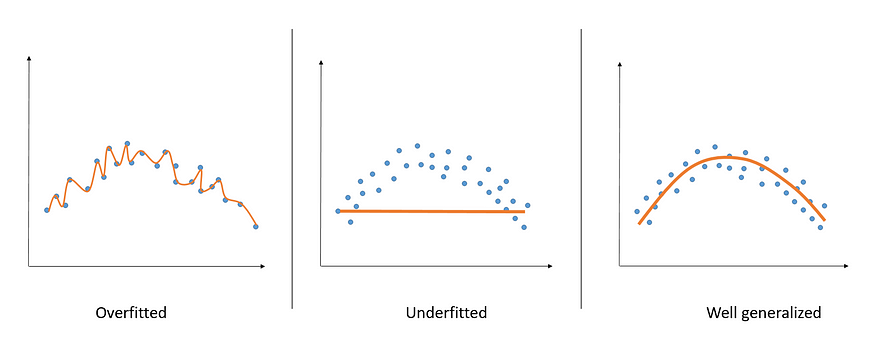
Một trong những nguyên nhân dẫn đến trạng thái over-fitting kể trên có thể xuất phát từ dữ liệu được sử dụng để huấn luyện mạng. Trước hết chúng ta cần nhắc lại một chút về những yêu cầu của một tập dữ liệu được coi là tốt khi sử dụng trong việc huấn luyện các mạng Deep Learning. Một tập dữ liệu được coi là tốt thường mang 3 đặc điểm sau:

• Sự đa dạng - Variety: Một tập dữ liệu huấn luyện tốt cần phải biểu diễn được đa dạng các hình thái trong domain của bài toán yêu cầu.
• Sự chính xác - Validity: tập dữ liệu phải được gán nhãn một cách chính xác dựa trên các vấn đề mà bài toán cần giải quyết
• Số lượng đủ lớn - Volume: Một tập dữ liệu để huấn luyện các mô hình Deep Learning phải đảm bảo một lượng dữ liệu lớn nhất định để đảm bảo mô hình có hiệu quả tốt nhất.

Xuất phát từ các yêu cầu dữ liệu đó, người ta nghĩ ra nhiều phương pháp để gia tăng số lượng các ảnh trong tập dữ liệu và từ đó các phương pháp Data Augmentation được xem xét đến trong quy trình xây dựng tập dữ liệu. Chúng ta có thể kể đến một số phương pháp đơn giản và minh hoạ nó như sau:

Di chuyển hình ảnh theo chiều ngang hoặc dọc

Với phương pháp này chúng ta có thể định nghĩa một tỉ lệ phần trăm (có thể được lựa chọn ngẫu nhiên) các pixels sẽ di chuyển lên xuống hoặc trái phải nhằm tạo ra ảnh mới từ ảnh ban đầu. Chúng ta có thể minh hoạ nó trong hình dưới đây

Di chuyển theo hướng trái phải

Hoặc di chuyển theo chiều lên xuống

Lật ảnh - flipping image

Chúng ta có thể sử dụng kĩ thuật lật ảnh trái phải hoặc trên dưới. Lưu ý là tuỳ từng bài toán chúng ta mới áp dụng kĩ thuật này. Không phải bài toán nào cũng có thể áp dụng được. Chỉ những đối tượng có tính chất đối xứng chúng ta mới nên áp dụng kĩ thuật này

Flip theo chiều ngang

Hoặc flip theo chiều dọc

Xoay ảnh - Rotating image

Chúng ta có thể xoay ảnh theo một góc nhất định để tạo ra các ảnh mới

Phóng to ảnh - Zoom image

Chúng ta cũng có thể phỏng to một phần của ảnh để tạo ra một ảnh mới

Đó là một số phương pháp cơ bản. Trong bài này chúng ta sẽ không đi sâu vào việc giải thích các phương pháp này cụ thể làm những việc gì. Chúng ta chỉ cần nắm được tư tưởng chính của Data Augmentation là được rồi. OK tiếp tục nhé

Empirical Risk Minimization - ERM

Trong các bài toán học có giám sát supervised learning, mục tiêu của chúng ta là đi tìm kiếm một hàm $f \in \mathcal{F}$ nhằm describe mối liên hệ giữa một random feature vector $X$ và một random target vector $Y$ tuân theo một phân phối xác suất kết hợp (joint distribution) $P(X, Y)$. Để thực hiện điều đó chúng ta sẽ cần định nghĩa một loss function $\ell$. Hàm loss này sẽ phạt những sự khác biệt giữa kết quả dự đoán của mô hình $f(x)$ và giá trị thật của target $y$. Giả sử $\left ( x, y \right )\sim P$. Khi chúng ta minimize hàm loss function $\ell$ thông qua data distribution $P$ thfi giá trị rủi ro kì vọng được định nghĩa

$R(f)=\int \ell(f(x), y) \mathrm{d} P(x, y)$

Tuy nhên trên thực tế, chúng ta rất ít khi biết được chính xác phân phối $P$ là gì. Thay vào đó chúng ta sẽ sử dụng một tâp hợp nhỏ để làm dữ liệu huấn luyện $\mathcal{D}=\left\{\left(x_{i}, y_{i}\right)\right\}_{i=1}^{n}$ trong đó $\left ( x_i, y_i \right )\sim P$ với $i=1...n$. sử dụng dữ liệu huấn luyện $\mathcal{D}$, chúng ta có thể xấp xỉ phân phối $P$ bằng xác suất thực nghiệm empirical distribution

$P_{\delta}(x, y)=\frac{1}{n} \sum_{i=1}^{n} \delta\left(x=x_{i}, y=y_{i}\right)$

Sử dụng phân phối này chúng ta có thể xấp xỉ expected risk trong thực nghiệm hay còn được gọi là empirical risk được định nghĩa như sau:

$R_{\delta}(f)=\int \ell(f(x), y) \mathrm{d} P_{\delta}(x, y)=\frac{1}{n} \sum_{i=1}^{n} \ell\left(f\left(x_{i}\right), y_{i}\right)$

Việc học hàm $f$ bằng cách minimize hàm loss fucntion trên được gọi là Empirical Risk Minimization principle. Ta sẽ giải thích vì sao nó được gọi như vậy. Loss function còn được gọi là risk function (hàm rủi ro). Chữ empirical được thêm vào bởi vì risk function này được tính trung bình trên một tập dữ liệu hữu hạn. Vậy empirical risk minimization tức là tối thiểu hóa rủi ro trên một tập dữ liệu hữu hạn.. Mặc dù rất có hiệu quả trong việc tính toán nhưng bản thân empirical risk lại chỉ mô phỏng được hàm $f$ trong một tập hữu hạn các sample. Điều này dẫn đến một số các hạn chế. Và một hạn chế lớn nhất khi sử dụng ERM đó chính là mô hình của chúng ta sẽ memorize - tức nhớ toàn bộ dữ liệu training thay vì generalize - tổng quát hoá cho các dạng dữ liệu chưa gặp. Hiện tượng này còn được biết đến với cái tên quen thuộc là over-fitting.

Vicinal Risk Minimization - VRM

Để khắc phục những nhược điểm của ERM, VRM đã được đề xuất bởi nhóm nghiên cứu của Chapele và năm 2000. Theo đó VRM sẽ xấp xỉ phân phói $P$ như sau:

$P_{\nu}(\tilde{x}, \tilde{y})=\frac{1}{n} \sum_{i=1}^{n} \nu\left(\tilde{x}, \tilde{y} \mid x_{i}, y_{i}\right)$

Trong đó $\nu$ được gọi là vicinity distribution - phân phối lân cận. Nó cho biết xác suất để tìm thấy một điểm dữ liệu virtual feature-target $\left ( \widetilde{x}, \widetilde{y} \right )$ trong một lân cận của điểm dữ liệu training $\left ( x_i, y_i \right )$. Trong paper gốc tác giả đã sử dụng phân phối Gausian để làm phân phối lân cận và nó có dạng như sau:

$\nu\left(\tilde{x}, \tilde{y} \mid x_{i}, y_{i}\right)=\mathcal{N}\left(\tilde{x}-x_{i}, \sigma^{2}\right) \delta\left(\tilde{y}=y_{i}\right)$

Trên thực tế, điều này tương đương với việc thêm các Gausian noise vào trong training data. Chúng ta cũng có cách cách khác để tạo ra các vicinity distribution giống như việc tạo ra các mẫu mới bằng phương pháp lật ảnh, scale ảnh ... Đây chính là cơ sở lý thuyết cho các phương pháp Data augmentation trình bày ở phía trên.

Lúc này dataset của chúng ta có dạng

$\mathcal{D}_{\nu}:=\left \{ \left ( \widetilde{x}_i,\widetilde{y}_i \right ) \right \}^{m}_{i=1}$

Và chúng ta sẽ cực tiểu hoá hàm mục tiểu của VRM như sau:

$R_{\nu}(f)=\frac{1}{m} \sum_{i=1}^{m} \ell\left(f\left(\tilde{x}_{i}\right), \tilde{y}_{i}\right)$

Các vấn đề mà paper giải quyết

Đi một thôi một hồi chúng ta cũng đến được với phần chính. Rất đơn giản nhưng lại vô cùng hiệu quả.

Trong paper này tác giả để xuất một vincial distribution mới gọi là mixup. Nó có dạng như sau

$\mu\left(\tilde{x}, \tilde{y} \mid x_{i}, y_{i}\right)=\frac{1}{n} \sum_{j}^{n} \underset{\lambda}{\mathbb{E}}\left[\delta\left(\tilde{x}=\lambda \cdot x_{i}+(1-\lambda) \cdot x_{j}, \tilde{y}=\lambda \cdot y_{i}+(1-\lambda) \cdot y_{j}\right)\right]$

Trong đó $\lambda \sim Beta\left ( \alpha, \alpha \right )$ với $\alpha \in \left ( 0, \infty \right )$.

$\begin{aligned} &\tilde{x}=\lambda x_{i}+(1-\lambda) x_{j} \\ &\tilde{y}=\lambda y_{i}+(1-\lambda) y_{j} \end{aligned}$

Với $\left ( x_i, y_i \right )$ và $\left ( x_j, y_j \right )$ là hai cặp mẫu dữ liệu và label tương ứng được lấy ngẫu nhiên từ trong tập dữ liệu huấn luyện. Tham số $\lambda \in \left [ 0, 1 \right ]$. Mixup hyperparameter $\alpha$ kiểm soát mức độ interpolation giữa hai sample. Trong trường hợp $\alpha \rightarrow 0$ thì phân phối $P$ càng gần với ERM.

Nó đơn giản đến mức code cũng chỉ có một vài dòng được trích từ paper gốc của tác giả

Kết quả thí nghiệm

Kết quả cho thấy việc áp dụng mixup đã giúp cho các mô hình cũ cải thiện được đáng kể độ chính xác. Vì đây là một phương pháp Data Augmentation nên việc áp dụng có thể áp dụng với bất kì kiến trúc mạng nào. Chúng ta có thể xem xét kết quả thí nghiệm trong hình sau

Source code

Các bạn có thể tham khảo chính source code của tác giả được trình bày tại repo https://github.com/facebookresearch/mixup-cifar10

Kết luận

Mixup là một phương pháp rất đơn giản trong thực hành nhưng lại đem lại những hiệu quả rất đáng kể trong việc improve các bài toán image classification. Ngay từ khi xuất hiện nó đã ngay lập tức nhận được sự chú ý bởi tính đơn giản và hiệu quả của nó. Đó cũng là lý do mà cho đến thời điểm hiện tại paper này đạt được lượng citation là 2429. (Tham khảo Google Scholar)

References

1. mixup: BEYOND EMPIRICAL RISK MINIMIZATION
2. [Paper] Mixup: Beyond Empirical Risk Minimization (Image Classification)
3. FAST AI JOURNEY: COURSE V3. PART 2. LESSON 14.1.