Xin chào mọi người chúng ta lại quay trở lại với series về ML From Scratch và trong bài này chúng ta sẽ lại nói về một thuật toán đơn giản nhất của học máy áp dụng cho bài toán phân lớp nhị phân đó chính là Logistic Regression. Trong bài này chúng ta sẽ tiến hành giải thích sơ qua về lý thuyết và cách mà Logistic Regression hoạt động. Đồng thời, vẫn giống như các bài trước đó, chúng ta sẽ implement lại nó từ đầu để hiểu bản chất cũng như so sánh với thư viện SK-Learn. OK chúng ta bắt đàu thôi
Lý thuyết cơ bản
Logistic Regression là gì
Bài trước chúng ta đã tìm hiểu về Linear Regression và ứng dụng nó trong bài toán dự đoán giá nhà. Trong Linear Regression chúng ta thấy label của chúng ta là một continous variable và vì thế nên đầu ra của chúng ta sẽ là một số thực cụ thể. Tuy nhiên trên thực tế có những bài toán yêu cầu đầu ra là dạng categorical tức là các class cụ thể. Đây được gọi là bài toán phân loại (classification) dựa trên dữ liệu đầu vào. Trong trường hợp số lượng class đầu ra của mô hình phân loại là 2 class thì chúng ta có bài toán phân lớp nhị phân - binary classification. Logistic Regression chính là một mô hình cơ bản được sinh ra để giải quyết bài toán phân lớp nhị phân đó. Hiện nay, nó được sử dụng để làm baseline cho các mô hình phân lớp nhị phân vì khá trực quan và dễ hiểu.
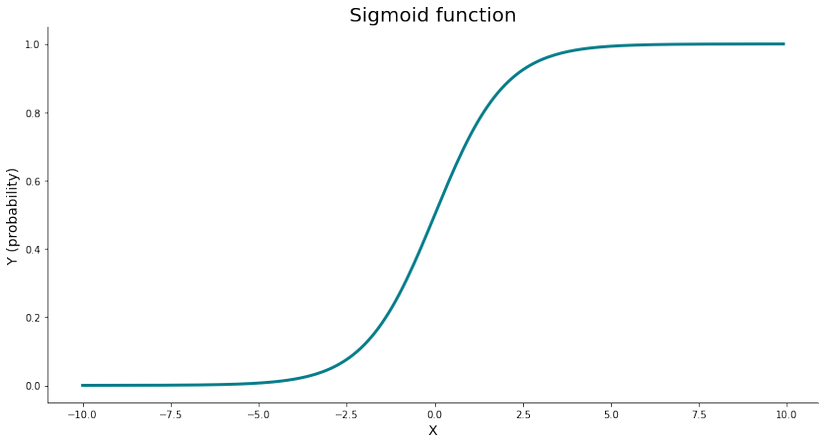
Về cơ bản thì Logistic Regression cũng gần giống như Linear Regression tức tìm một hàm tuyến tính để biểu diễn dữ liệu. Chỉ có điều đầu ra của Logistic Regression sẽ được đưa qua hàm sigmoid để đưa đầu ra về trong khoảng - thể hiện xác suất của đầu ra trên mỗi class. Hàm này được gọi là activation function có công thức như sau:
Nếu đầu ra của mạng sau khi đi qua hàm sigmoid lớn hơn một threshold nhất định thì chúng ta sẽ gắn giá trị cho class là 1, ngược lại sẽ là 0. Mình hoạ đầu ra của hàm sigmoid trong hình sau
Cập nhật trọng số
Giống như trong Linear Regression chúng ta cũng có hai tham số cần phải cần phải cập nhật. Các bạn có thể tham khảo lại phần cực tiểu hoá hàm loss trong bài trước để hiểu rõ hơn. Tuy nhiên có một điểm khác, do label của ta là một số cụ thể tức là class 0 hay class 1 thế nên chúng ta không nên sử dụng Mean Square Error để làm hàm loss được mà cần phải có một hàm loss khác. Chúng ta sẽ cùng nhau đi tìm hiểu hàm loss Binary Cross Entropy
Binary Cross Entropy Loss - BCE
Thay vào đó chúng ta sử dụng Binary Cross Entropy Loss để làm hàm loss cho bài toán này. BCE Loss hay còn được gọi là log loss có công thức như sau:
Để hiểu hơn về các khái niệm như Entropy, Cross Entropy, mình suggest các bạn đọc bài viết rất chi tiết của tác giả Nguyễn Thành Trung Entropy, Cross Entropy và KL Divergence. Quay trở lại với BCE, hàm loss này sẽ "phạt" đối với các wrong prediction nhiều hơn là "thưởng" cho các dự đoán đúng. Các bạn có thể xem xét các ví dụ sau:
Ví dụ 1: Nếu mô hình của bạn dự đoán 90% cho positive class và 10% cho negative class thì giá trị của BCE sẽ là bao nhiêu?
Áp dụng công thức chúng ta sẽ thu được kết quả là 0.10536

Ta thấy giá trị của hàm loss BCE khá nhỏ khoảng 0.1 bởi vì mô hình của chúng ta đang dự đoán đúng và khá tự tin với xác suất 90%. Tuy nhiên điều gì sẽ xảy ra nếu như mô hình rất tự tin nhưng vào class negative. Chúng ta sẽ cùng xét ví dụ thứ 2
- Ví dụ 2: Nếu mô hình của bạn dự đoán 10% cho positive class và 90% cho negative class thì giá trị của BCE sẽ là bao nhiêu?
Lúc này áp dụng công thức của BCE chúng ta sẽ thấy giá trị rất khác biệt. BCE có giá trị là 2.30259
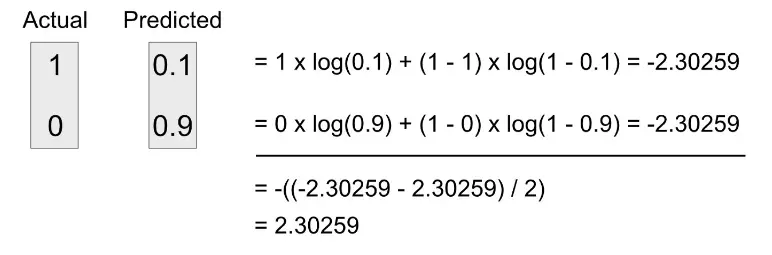
Điều này chứng tỏ rằng BCE có tác dụng phạt rất nặng các dự đoán sai của mô hình. Hàm loss này đặc biệt hữu ích với bài toán phân lớp nhị phân của chúng ta
Tính toán đạo hàm và cập nhật trọng số
Quay trở lại vấn đề tối ưu, mục tiêu của chúng ta là cực tiểu hoá giá trị của hàm loss BCE. Tuy nhiên như trong công thức phía trên chúng ta sẽ thấy rằng trong hàm loss BCE chứa hàm activation sigmoid. Trong hàm activation sigmoid lại chứa trọng số và bias . Vậy nên chúng ta muốn tính được đạo hàm của và thì sẽ cần phải áp dụng chain rule hay còn gọi là đạo hàm của hàm hợp.
Chain rule là phương pháp được áp dụng để tính toán đạo hàm của một hàm số mà bản thân nó chứa các hàm số khác. Có thể hình dung nó theo công thức tổng quát sau:
Như đã nói ở trên thì hàm loss của chúng ta ở trên chứa hàm sigmoid và hàm sigmoid lại chứa và nên chúng ta cần phải thực hiện 3 bước đạo hàm. Cụ thể như sau
- Bước 1: Tính . Bỏ qua dấu trong công thức của chúng ta có loss function với 1 sample
Xét đạo hàm của logarit chúng ta có:
Xét hai thành phần trong hàm loss phía trên chúng ta có
và
- Bước 2: Tính toán . Ta đặt
trong đó
Chúng ta có đạo hàm
Tổng hợp cả hai phần trên chúng ta có

- Bước 3: Tính toán . Chúng ta có
Vậy nên ta có đạo hàm
Tổng hợp đạo hàm của các hàm hợp trên chúng ta có
Rất đẹp phải không các bạn. Vậy là chúng ta đã xong phần khó nhất rồi, giờ chỉ là implement lại thôi
Implement với Numpy
Thử nghiệm hàm loss BCE
Đầu tiên chúng ta cùng nhau thử nghiệm thuật toán Binary Cross entropy trước nhé. Có công thức rồi việc của chúng ta code theo thôi
def bce(y_true, y_pred):
def safe_log(x):
return np.log(x) if x != 0 else 0
bce_loss = 0
for cur_y_true, cur_y_pred in zip(y_true, y_pred):
bce_loss += cur_y_true*safe_log(cur_y_pred) + (1 - cur_y_true)*safe_log(1 - cur_y_pred)
return -bce_loss / len(y_true)
Hãy cùng thử một số ví dụ sau với hàm bce() phía trên
bce([1, 0], [0.9, 0.1])
>>> 0.10536051565782628
bce([1, 0], [0.1, 0.9])
>>> 2.302585092994046
bce([1, 0], [0.3, 0.7])
>>> 1.203972804325936
Implement mô hình Logistic Regression
class LogisticRegression:
def __init__(self, lr=0.01, epochs=1000):
self.epochs = epochs
self.lr = lr
self.W = 0
def initialize(self, n_features):
self.W = np.random.normal(0, 1, size=(n_features, 1))
self.W = np.squeeze(self.W, axis=1)
def sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def bce(self, y_true, y_pred):
def safe_log(x):
return np.log(x) if x != 0 else 0
bce_loss = 0
for cur_y_true, cur_y_pred in zip(y_true, y_pred):
bce_loss += cur_y_true*safe_log(cur_y_pred) + (1 - cur_y_true)*safe_log(1 - cur_y_pred)
return -bce_loss / len(y_true)
def gradient(self, X, y, n_samples):
y_pred = self.sigmoid(np.dot(X, self.W))
d_w = np.dot(X.T, y_pred - y) / n_samples
return d_w
def fit(self, X, y):
losses = []
# Load sample and features
n_samples, n_features = X.shape
# Init weights
self.initialize(n_features)
# Calculate gradient descent per epoch
for _ in tqdm(range(self.epochs)):
y_pred = self.sigmoid(np.dot(X, self.W))
d_w = self.gradient(X, y, n_samples)
self.W -= self.lr * d_w
loss = self.bce(y, y_pred)
losses.append(loss)
print('Loss: ', loss)
def predict(self, X):
return [1 if i > 0.5 else 0 for i in self.sigmoid(np.dot(X, self.W))]
Như trên đoạn code trên chúng ta để ý thấy việc cập nhật đạo hàm được tính toán theo giải thuật Gradient Descent quen thuộc. Phần cập nhật trọng số được tính như sau
d_w = self.gradient(X, y, n_samples)
self.W -= self.lr * d_w
trong đó hàm gradient được tính toán theo công thức được đã chứng minh phía trên
Chạy thử với dữ liệu cancer
Chúng ta sử dụng thử viên sklearn để load bộ dữ liệu này
import sklearn.datasets
import pandas as pd
from sklearn.model_selection import train_test_split
cancer = sklearn.datasets.load_breast_cancer()
data = pd.DataFrame(cancer.data, columns = cancer.feature_names)
data["label"] = cancer.target
data.head()
Mình sẽ không trình bày chi tiết về bộ dữ liệu này nữa. Các bạn có thể tự tham khảo trên mạng. Đầu tiên chúng ta cần normalize data và tiến hành chia train/test
X = data.iloc[:,:-1] #all rows, all columns except the last
y = data.iloc[:,-1] # all rows, only the last column
X = MinMaxScaler().fit_transform(X)
X_train, X_test, Y_train, Y_test = train_test_split(X,y, test_size = 0.30, random_state = 1)
Sau đó chúng ta tiến hành training mô hình
model = LogisticRegression(lr=0.1, epochs=20000)
model.fit(X_train, Y_train)
Chúng ta đợi model training xong sẽ thu được kết quả
100%|██████████| 20000/20000 [00:53<00:00, 372.38it/s]
Loss: 0.1515871134230394
Đánh giá mô hình
Sau khi mô hình đã training xong thì tiến hành kiếm tra đánh giá mô hình trên tập test
Y_pred = model.predict(X_test)
print(classification_report(Y_test, Y_pred))
chúng ta thu được kết quả sau
precision recall f1-score support
0 0.93 0.84 0.88 63
1 0.91 0.96 0.94 108
accuracy 0.92 171
macro avg 0.92 0.90 0.91 171
weighted avg 0.92 0.92 0.92 171
Độ chính xác khoảng 92%
So sánh với SkLearn
Giờ chúng ta sẽ chạy thử với model của SKLearn đẻ so sánh kết quả
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=0).fit(X_train, Y_train)
Y_pred_sk = clf.predict(X_test)
print(classification_report(Y_test, Y_pred_sk))
Thu được kết quả trên sklearn rất tốt khoảng 97%
precision recall f1-score support
0 1.00 0.90 0.95 63
1 0.95 1.00 0.97 108
accuracy 0.96 171
macro avg 0.97 0.95 0.96 171
weighted avg 0.97 0.96 0.96 171
Kết luận
Chúng ta đã cùng nhau implement một thuật toán rất đơn giản trong Machine Learning đó là Logistic Regression sử dụng trong bài toán phân lớp nhị phân sử dụng Binary Cross Entropy Loss. Hi vọng qua bài viết này các bạn sẽ hiểu rõ hơn về thuật toán này. Các bạn có thể tham khảo source code trong bài tại đây. Hẹn gặp lại các bạn trong những bài viết sau.