Giới thiệu

• Là lập trình viên chắc hẳn chúng ta đã nghe về đệ quy, vậy đệ quy là gì?
• Đệ quy là một mẫu lập trình hữu ích trong các trường hợp khi một tác vụ có thể được chia thành nhiều tác vụ cùng loại, nhưng đơn giản hơn một cách tự nhiên. Hoặc khi một nhiệm vụ có thể được đơn giản hóa thành một hành động dễ dàng cộng với một đối số đơn giản hơn của cùng một nhiệm vụ. Hoặc, như chúng ta sẽ thấy ngay sau đây, để xử lý các cấu trúc dữ liệu nhất định. Khi một hàm giải quyết một nhiệm vụ, trong quá trình đó nó có thể gọi nhiều hàm khác. Một phần của trường hợp này là khi một hàm gọi chính nó . Đó được gọi là đệ quy.

Nội dung

Hai cách suy nghĩ

• Đối với một cái gì đó đơn giản để bắt đầu - hãy viết một hàm pow(x, n) - tính lũy thùy bậc n của x. Nói cách khác, nhân với x chính nó n lần.

pow(2, 2) = 4
pow(2, 3) = 8
pow(2, 4) = 16

• Có hai cách để thực hiện hàm này:

1. Vòng lặp for:

function pow(x, n) {
  let result = 1;

  // nhân x n lần trong vòng lặp
  for (let i = 0; i < n; i++) {
    result *= x;
  }

  return result;
}

alert( pow(2, 3) ); // 8

2. Sử dụng đệ quy: gọi lại chính hàm đó

function pow(x, n) {
  if (n == 1) {
    return x;
  } else {
    return x * pow(x, n - 1);
  }
}

alert( pow(2, 3) ); // 8

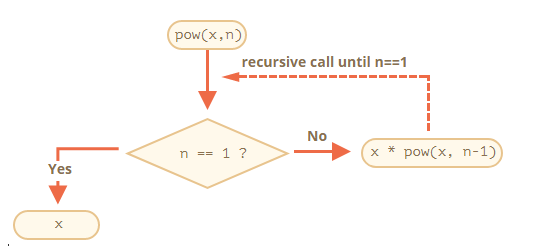
• Xin lưu ý rằng đối số đệ quy khác về cơ bản như thế nào. Khi pow(x, n) được gọi, việc thực thi chia thành hai nhánh:

              if n==1  = x
             /
pow(x, n) =
             \
              else     = x * pow(x, n - 1)

• Nếu n == 1, thì mọi thứ thật tầm thường. Nó được gọi là cơ sở của đệ quy, bởi vì nó ngay lập tức tạo ra kết quả hiển nhiên: pow(x, 1) bằng x.

• Nếu không, chúng ta có thể đại diện pow(x, n) là bằng x * pow(x, n - 1). Trong toán học, người ta viết x^n = x * x^(n-1). Đây được gọi là bước đệ quy: chúng ta chuyển nhiệm vụ thành một hành động đơn giản hơn (nhân bởi x) và một lệnh gọi hàm đơn giản hơn của cùng một tác vụ (lũy thừa thấp hơn là n - 1). Các bước tiếp theo đơn giản hóa nó hơn và xa hơn cho đến khi đạt được n bằng 1.

• Chúng ta cũng có thể nói rằng pow đệ quy gọi chính nó đến n == 1.

• Ví dụ: để tính toán pow(2, 4) dùng đệ quy, hãy thực hiện các bước sau:

pow(2, 4) = 2 * pow(2, 3)
pow(2, 3) = 2 * pow(2, 2)
pow(2, 2) = 2 * pow(2, 1)
pow(2, 1) = 2

• Vì vậy, đệ quy làm giảm một lời gọi hàm thành đơn giản hơn, và càng đơn giản hơn... cho đến khi kết quả trở nên rõ ràng.

Đệ quy thường ngắn hơn

• Một giải pháp đệ quy thường ngắn hơn một giải pháp lặp lại.
• Ở đây chúng ta có thể viết lại tương tự bằng cách sử dụng toán tử điều kiện ? thay vì if để làm cho pow(x, n) ngắn gọn hơn và vẫn rất dễ đọc:

function pow(x, n) {
  return (n == 1) ? x : (x * pow(x, n - 1));
}

• Số lệnh gọi lồng nhau tối đa (bao gồm lệnh gọi đầu tiên) được gọi là độ sâu đệ quy (recursion depth). Trong trường hợp của chúng tôi, nó sẽ chính xác n.
• Độ sâu đệ quy tối đa bị giới hạn bởi công cụ JavaScript. Chúng ta có thể tin rằng nó là 10000, một số động cơ cho phép nhiều hơn, nhưng 100000 có lẽ là quá giới hạn đối với đa số chúng. Có những tính năng tối ưu hóa tự động giúp giảm bớt điều này (tối ưu hóa lời gọi cuối), nhưng chúng chưa được hỗ trợ ở mọi nơi và chỉ hoạt động trong những trường hợp đơn giản.
• Điều đó hạn chế việc áp dụng đệ quy, nhưng nó vẫn còn rất rộng. Có rất nhiều tác vụ mà cách suy nghĩ đệ quy đưa ra mã đơn giản hơn, dễ bảo trì hơn.

Bối cảnh thực thi và ngăn xếp

• Bây giờ chúng ta hãy kiểm tra cách hoạt động của các cuộc gọi đệ quy. Đối với điều đó, chúng ta sẽ xem xét bên dưới các chức năng.
• Thông tin về quá trình thực thi một chức năng đang chạy được lưu trữ trong ngữ cảnh thực thi của nó .
• Các bối cảnh thực hiện là một cấu trúc dữ liệu nội bộ có chứa thông tin chi tiết về việc thực hiện một chức năng: nơi kiểm soát dòng chảy hiện nay, các biến hiện tại, giá trị của this (chúng ta không sử dụng nó ở đây) và vài chi tiết nội bộ khác.
• Một lệnh gọi hàm có chính xác một ngữ cảnh thực thi được liên kết với nó.
• Khi một hàm thực hiện một cuộc gọi lồng nhau, điều sau sẽ xảy ra:
  • Chức năng hiện tại bị tạm dừng.
  • Bối cảnh thực thi được liên kết với nó được ghi nhớ trong một cấu trúc dữ liệu đặc biệt được gọi là ngăn xếp ngữ cảnh thực thi.
  • Cuộc gọi lồng nhau thực thi.
  • Sau khi nó kết thúc, ngữ cảnh thực thi cũ được truy xuất từ ngăn xếp và chức năng bên ngoài được tiếp tục lại từ nơi nó đã dừng.
• Hãy xem những gì sẽ xảy ra trong hàm pow(2, 3):

pow(2, 3)

1 function pow(x, n) {
2   if (n == 1) {
3    return x;
4   } else {
5     return x * pow(x, n - 1);
6   }
7 }
8 
9 alert(pow(2, 3));

• Trong phần đầu của cuộc gọi pow(2, 3), ngữ cảnh thực thi sẽ lưu trữ các biến x = 2, n = 3, luồng thực thi nằm ở dòng 1 của hàm. Chúng ta có thể phác thảo nó như là:

Ngữ cảnh: {x: 2, n: 3, dòng 1} // gọi: pow(2, 3)

• Đó là khi hàm bắt đầu thực thi. Điều kiện n == 1 là sai, vì vậy luồng tiếp tục vào nhánh thứ hai của if. Các biến giống nhau, nhưng dòng thay đổi, vì vậy bối cảnh bây giờ là:

Ngữ cảnh: {x: 2, n: 3, dòng 5} // gọi: pow(2, 3)

• Để tính toán x * pow(x, n - 1), chúng ta cần tạo một cuộc gọi con pow với các đối số mới pow(2, 2).

pow(2, 2)

• Để thực hiện một cuộc gọi lồng nhau, JavaScript ghi nhớ ngữ cảnh thực thi hiện tại trong ngăn xếp ngữ cảnh thực thi.
• Ở đây chúng ta gọi cùng một hàm pow, nhưng nó hoàn toàn không quan trọng. Quá trình này giống nhau cho tất cả các chức năng:
  • Bối cảnh hiện tại được "ghi nhớ" ở trên cùng của ngăn xếp.
  • Bối cảnh mới được tạo cho cuộc gọi con.
  • Khi cuộc gọi con kết thúc - ngữ cảnh trước đó được bật ra từ ngăn xếp và quá trình thực thi của nó vẫn tiếp tục.
• Đây là ngăn xếp ngữ cảnh khi chúng ta nhập cuộc gọi con pow(2, 2):

Ngữ cảnh: {x: 2, n: 2, tại dòng 1} // gọi: pow(2, 2)

Ngữ cảnh: {x: 2, n: 3, tại dòng 5} // gọi: pow(2, 3)

• Bối cảnh thực thi hiện tại mới ở trên cùng (và in đậm), và các ngữ cảnh được ghi nhớ trước đó ở bên dưới. Khi chúng ta hoàn thành lệnh gọi con - thật dễ dàng để tiếp tục ngữ cảnh trước đó, vì nó giữ cả hai biến và vị trí chính xác của mã nơi nó đã dừng (2 * pow(2, 2)).

Lưu ý: Ở đây trong code, chúng ta sử dụng từ “dòng”, như trong ví dụ của chúng ta chỉ có một cuộc gọi con trong một dòng, nhưng nhìn chung một dòng mã có thể chứa nhiều cuộc gọi con, chẳng hạn như pow(…) + pow(…) + somethingElse(…). Vì vậy, sẽ chính xác hơn nếu nói rằng quá trình thực thi tiếp tục “ngay sau lệnh gọi con”.

pow (2, 1)

• Quá trình này lặp đi lặp lại: một subcall mới được thực hiện tại dòng 5, bây giờ với đối số x=2, n=1. Một ngữ cảnh thực thi mới được tạo, bối cảnh trước đó được đẩy lên trên cùng của ngăn xếp:

Ngữ cảnh: {x: 2, n: 1, tại dòng 1} // gọi: pow(2, 1)

Ngữ cảnh: {x: 2, n: 2, tại dòng 5} // gọi: pow(2, 2)

Ngữ cảnh: {x: 2, n: 3, tại dòng 5} // gọi: pow(2, 3)

• Hiện có 2 ngữ cảnh cũ và 1 ngữ cảnh hiện đang chạy cho lời gọi pow(2, 1).
• Trong quá trình thực hiện pow(2, 1), không giống như các lần gọi trước, điều kiện n == 1 đúng, vì vậy nhánh if đầu tiên hoạt động (return x). Không còn lời gọi lồng nhau nữa, vì vậy hàm kết thúc, trả về 2.
• Khi hàm kết thúc, ngữ cảnh thực thi của nó không còn cần thiết nữa, vì vậy nó sẽ bị xóa khỏi bộ nhớ. Phần trước đó được khôi phục ở phía trên cùng của ngăn xếp:

Ngữ cảnh: {x: 2, n: 2, tại dòng 5} // gọi: pow(2, 2)

Ngữ cảnh: {x: 2, n: 3, tại dòng 5} // gọi: pow(2, 3)

• Quá trình thực hiện pow(2, 2) được tiếp tục. Nó có kết quả của cuộc gọi con pow(2, 1), vì vậy nó cũng có thể kết thúc việc đánh giá x * pow(x, n - 1), trả về 4.
• Sau đó, ngữ cảnh trước đó được khôi phục:

Ngữ cảnh: {x: 2, n: 3, tại dòng 5} // gọi: pow(2, 3)

• Khi nó kết thúc, chúng tôi có kết quả là pow(2, 3) = 8. Độ sâu đệ quy trong trường hợp này là 3. Như chúng ta có thể thấy từ các phần code minh họa ở trên, độ sâu đệ quy bằng với số ngữ cảnh tối đa trong ngăn xếp.
• Lưu ý các yêu cầu về bộ nhớ. Bối cảnh chiếm bộ nhớ. Trong trường hợp của chúng ta, việc nâng lên lũy thừa của n thực sự yêu cầu bộ nhớ cho n cho các ngữ cảnh, cho tất cả các giá trị thấp hơn của n.
• Thuật toán dựa trên vòng lặp tiết kiệm bộ nhớ hơn:

function pow(x, n) {
  let result = 1;

  for (let i = 0; i < n; i++) {
    result *= x;
  }

  return result;
}

• Phép lặp pow sử dụng một ngữ cảnh duy nhất đang thay đổi i và result trong quá trình lặp. Yêu cầu bộ nhớ của nó là nhỏ, cố định và không phụ thuộc vào n.
• Bất kỳ đệ quy nào cũng có thể được viết lại dưới dạng một vòng lặp. Biến thể vòng lặp thường có thể được thực hiện hiệu quả hơn.
• … Nhưng đôi khi việc viết lại không hề nhỏ, đặc biệt khi hàm sử dụng các lệnh gọi con đệ quy khác nhau tùy thuộc vào điều kiện và kết hợp các kết quả của chúng hoặc khi phân nhánh phức tạp hơn. Và việc tối ưu hóa có thể không cần thiết và hoàn toàn không đáng với những nỗ lực. Đệ quy có thể cho một đoạn mã ngắn hơn, dễ hiểu hơn và dễ hỗ trợ hơn. Tối ưu hóa không bắt buộc ở mọi nơi, chủ yếu là chúng ta cần một mã tốt, đó là lý do tại sao nó được sử dụng.

Duyệt đệ quy

• Một ứng dụng tuyệt vời khác của đệ quy là duyệt đệ quy. Giả sử chúng ta có một công ty. Cơ cấu nhân viên có thể được trình bày dưới dạng một đối tượng:

let company = {
  sales: [{
    name: 'John',
    salary: 1000
  }, {
    name: 'Alice',
    salary: 1600
  }],

  development: {
    sites: [{
      name: 'Peter',
      salary: 2000
    }, {
      name: 'Alex',
      salary: 1800
    }],

    internals: [{
      name: 'Jack',
      salary: 1300
    }]
  }
};

• Nói cách khác, một công ty có các phòng ban.
  • Một bộ phận có thể có một loạt các nhân viên. Ví dụ, bộ phận sales có 2 nhân viên: John và Alice.
  • Hoặc một bộ phận có thể chia thành các phân khu, như development có hai chi nhánh: sites và internals. Mỗi người trong chúng có nhân viên riêng của họ.
• Bây giờ, giả sử chúng ta muốn một hàm lấy tổng tất cả các khoản lương. Làm thế nào chúng ta có thể làm điều đó?
• Ý tưởng đầu tiên có thể là tạo một vòng lặp for với vòng lặp con company lồng nhau trên các phòng ban cấp 1. Nhưng sau đó chúng ta cần nhiều vòng lặp con lồng nhau hơn để lặp lại các nhân viên trong các phòng ban cấp 2 như sites… Và sau đó một vòng lặp con khác bên trong các vòng lặp con dành cho các phòng ban cấp 3 có thể xuất hiện trong tương lai? Nếu chúng ta đặt 3-4 vòng con lồng nhau trong mã để duyệt qua một đối tượng duy nhất, nó sẽ trở nên khá xấu xí.
• Hãy thử đệ quy. Như chúng ta có thể thấy, khi hàm của chúng ta nhận được một bộ phận để tổng hợp, có hai trường hợp có thể xảy ra:
  • Hoặc đó là một bộ phận “đơn giản” với nhiều người - sau đó chúng ta có thể tính tổng tiền lương trong một vòng lặp đơn giản.
  • Hoặc đó là một đối tượng có các Nkhoang con - sau đó chúng ta có thể thực hiện N các cuộc gọi đệ quy để lấy tổng cho mỗi khoang con và kết hợp các kết quả.
• Thuật toán có lẽ thậm chí còn dễ đọc hơn từ code:

let company = { // đối tượng
  sales: [{name: 'John', salary: 1000}, {name: 'Alice', salary: 1600 }],
  development: {
    sites: [{name: 'Peter', salary: 2000}, {name: 'Alex', salary: 1800 }],
    internals: [{name: 'Jack', salary: 1300}]
  }
};

// Hàm tính tổng lương
function sumSalaries(department) {
  if (Array.isArray(department)) { // case (1)
    return department.reduce((prev, current) => prev + current.salary, 0); // tính tổng lương cho trường hợp là một mảng
  } else { // case (2)
    let sum = 0;
    for (let subdep of Object.values(department)) {
      sum += sumSalaries(subdep); // lời gọi đệ quy
    }
    return sum;
  }
}

alert(sumSalaries(company)); // 7700

• Chúng ta có thể dễ dàng nhận thấy nguyên tắc: đối với một đối tượng, với {...} lệnh gọi con được tạo ra, trong khi các mảng [...] là “lá” của cây đệ quy, chúng cho kết quả ngay lập tức.

Cấu trúc đệ quy

• Cấu trúc dữ liệu đệ quy (được định nghĩa đệ quy) là cấu trúc tự sao chép thành từng phần. Để hiểu rõ hơn, chúng tôi sẽ đề cập đến một cấu trúc đệ quy khác có tên là “Danh sách được liên kết” có thể là một giải pháp thay thế tốt hơn cho mảng trong một số trường hợp.

Danh sách liên kết (Linked List)

• Hãy tưởng tượng, chúng ta muốn lưu trữ một danh sách các đối tượng có thứ tự. Lựa chọn tự nhiên sẽ là một mảng:

let arr = [obj1, obj2, obj3];

• … Nhưng có một vấn đề với các mảng. Các thao tác “xóa phần tử” và “chèn phần tử” rất tốn kém. Ví dụ: arr.unshift(obj) hoạt động phải đánh số lại tất cả các phần tử để nhường chỗ cho một phần tử mới objvà nếu mảng lớn, thì sẽ mất thời gian. Tương tự với arr.shift().
• Các thay đổi chỉ cấu trúc mà không đòi hỏi hàng loạt renumbering là những hành động với chỉ số cuối của mảng: arr.push/pop. Vì vậy, một mảng có thể khá chậm đối với các hàng đợi lớn, khi chúng ta phải làm việc với các chỉ số đầu của mảng.
• Ngoài ra, nếu chúng ta thực sự cần chèn / xóa nhanh, chúng ta có thể chọn một cấu trúc dữ liệu khác được gọi là linked list (danh sách liên kết). Phần tử danh sách liên kết được định nghĩa một cách đệ quy là một đối tượng với:
  • value
  • Thuộc tính next tham chiếu đến phần tử danh sách được liên kết tiếp theo hoặc null nếu đó là phần cuối.
• Ví dụ:

let list = {
  value: 1,
  next: {
    value: 2,
    next: {
      value: 3,
      next: {
        value: 4,
        next: null
      }
    }
  }
};

• Biểu diễn đồ họa của danh sách:
• Mã code thay thế:

let list = {value: 1};
list.next = {value: 2};
list.next.next = {value: 3};
list.next.next.next = {value: 4};
list.next.next.next.next = null;

• Ở đây chúng ta thậm chí có thể thấy rõ ràng hơn rằng có nhiều đối tượng, mỗi đối tượng có value và con trỏ next đến hàng xóm. Biến list là đối tượng đầu tiên trong chuỗi, vì vậy con trỏ next sau nó có thể đến bất cứ phần tử nào mới.

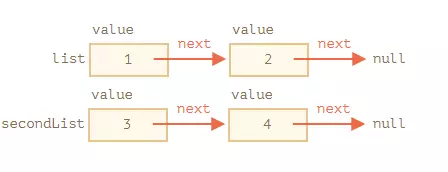
• Danh sách có thể dễ dàng được chia thành nhiều phần và sau đó được nối lại:

• Liên kết:

list.next.next = secondList;

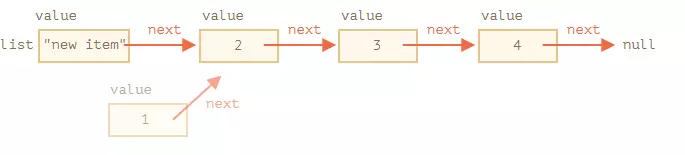
• Và chắc chắn chúng ta có thể chèn hoặc loại bỏ các mục ở bất kỳ nơi nào. Ví dụ để thêm một phần tử ở đầu:

let list = {value: 1};
list.next = {value: 2};
list.next.next = {value: 3};
list.next.next.next = {value: 4};

// thêm phần tử ở đầu danh sách
list = {value: "new item", next: list};

• Để xóa một giá trị ở giữa, hãy thay đổi giá trị next trước đó:

list.next = list.next.next;

• Không giống như mảng, không có đánh số lại hàng loạt, chúng ta có thể dễ dàng sắp xếp lại các phần tử trong danh sách. Đương nhiên, danh sách không phải lúc nào cũng tốt hơn mảng. Nếu không, mọi người sẽ chỉ sử dụng danh sách.
• Hạn chế chính là chúng ta không thể dễ dàng truy cập một phần tử theo số của nó. Trong một mảng dễ dàng: arr[n] là một tham chiếu trực tiếp. Nhưng trong danh sách, chúng ta cần bắt đầu từ mục đầu tiên và đi next N lần lượt để lấy phần tử thứ N.
• … Nhưng không phải lúc nào chúng ta cũng cần những thao tác như vậy. Ví dụ, khi chúng ta cần một queue hoặc thậm chí một deque - cấu trúc có thứ tự phải cho phép thêm / bớt phần tử rất nhanh từ cả hai đầu, nhưng không cần truy cập vào phần giữa của nó.
• Danh sách có thể được nâng cao:
  • Chúng ta có thể thêm thuộc tính prev ngoài thuộc tính next để tham chiếu đến phần tử trước đó, giúp di chuyển trở lại một cách dễ dàng.
  • Chúng ta cũng có thể thêm một biến có tên tail tham chiếu đến phần tử cuối cùng của danh sách (và cập nhật nó khi thêm / bớt các phần tử từ cuối).
  • … Cấu trúc dữ liệu có thể thay đổi tùy theo nhu cầu của chúng ta.

Tổng kết

• Đệ quy là một thuật ngữ lập trình có nghĩa là gọi một hàm từ chính nó. Các hàm đệ quy có thể được sử dụng để giải quyết các tác vụ theo những cách dễ hiểu.
• Khi một hàm gọi chính nó, đó được gọi là bước đệ quy. Cơ sở của đệ quy là các đối số của hàm làm cho nhiệm vụ đơn giản đến mức hàm không thực hiện thêm các lệnh gọi.
• Một đệ quy được định nghĩa cấu trúc dữ liệu là một cấu trúc dữ liệu có thể được định nghĩa bằng chính nó (linked list).
• Bất kỳ hàm đệ quy nào cũng có thể được viết lại thành một hàm lặp. Và điều đó đôi khi được yêu cầu để tối ưu hóa mọi thứ. Nhưng đối với nhiều tác vụ, một giải pháp đệ quy đủ nhanh và dễ dàng hơn để viết và hỗ trợ.
• Nguồn tham khảo: https://javascript.info/recursion