Skip to content

Dashboard

[AI From Scratch] [Basic ML] #2 - Linear Regression

Created by Admin

Xin chào mọi người chúng ta lại quay trở lại với series về ML From Scratch và trong bài này chúng ta sẽ lại nói về một thuật toán vô cùng đơn giản nhưng rất hiệu quả trong nhiều bài toán của Học máy đó chính là Linear Regresion. Chúng ta sẽ bắt đầu bằng cách giải thích một cách dễ hiểu nhất về Linear Regresion và các ứng dụng của nó nhé.

Ví dụ về định giá nhà đất

Đây có thể coi là một ví dụ kinh điển mà bạn chắc chắn sẽ từng gặp qua khi tìm hiểu về bài toán Linear Regresion. Giả sử một ngôi nhà có giá là yy và có các thuộc tính đại diện cho diện tích, số tầng, khoảng cách đến trung tâm ... lần lượt là x1,x2,...,xnx_1, x_2, ..., x_n. Chúng ta mong muốn tìm được một hàm tuyến tính biểu diễn mối tương quan này như sau

y^=Wx+b\hat{y} = Wx + b

Trong đó ma trận WW được gọi là weight và vector bb được gọi là bias.

Có thể hình dung hàm này bằng biểu diễn hình học như sau

Trong không gian hai chiều, có thể tưởng tượng rằng chúng ta đang tìm một đường thẳng gần nhất với tất cả các điểm trong tập dữ liệu training và kì vọng rằng nó cũng có thể gần nhất với các điểm dữ liệu chưa gặp trong tương lai.

Nhắc lại một chút về lý thuyết

Cách định nghĩa hàm loss

Để định nghĩa khái niệm gần ở phía trên chúng ta có sử dụng Mean Square Error Loss được định nghĩa như công thức sau:

MSE=1N∑i=1N(yi−yi^)2MSE=\frac{1}{N}\sum_{i=1}^{N}(y_i - \hat{y_i})^{2}

Hay chúng ta có thể viết lại như sau

MSE=J(W,b)=1N∑i=1N(yi−(Wxi+b))MSE=J(W, b) = \frac{1}{N}\sum_{i=1}^{N}(y_i - (Wx_i + b))

Cực tiểu hoá hàm loss

Chúng ta cần cực tiểu hoá hàm lỗi này với các tham số cần tìm là WW và bb chúng ta có thể coi nó như một hàm 2 biến. Để tìm cực trị của hàm này trước hết cần phải xét các điểm dừng tức là giải hệ phương trình các đạo hàm riêng bằng 0. Người ta còn gọi các điểm dừng này là local minimum hay cực trị địa phương để phân biệt với global minimum - còn gọi là cực tiểu của hàm số (tức tại điểm đó hàm số đại giá trị nhỏ nhất). Dễ thấy global minimum là một trường hợp đặc biệt của local minimum và cũng chính là bộ tham số mà chúng ta đang kì vọng tìm được trong các bài toán Machine Learning. Quay trở lại với Linear Regression. Ta có các đạo hàm riêng của hàm loss LL như sau

J′(W,b)=[dJdWdJdb]=[1N∑−2xi(yi−(Wxi+b))1N∑−2(yi−(Wxi+b))]=[1N∑2xi(y^i−yi)1N∑2(y^i−yi)]J'(W, b) = \begin{bmatrix} \frac{dJ}{dW} \\ \\ \frac{dJ}{db} \end{bmatrix} = \begin{bmatrix} \frac{1}{N}\sum -2x_i(y_i - (Wx_i + b)) \\ \\ \frac{1}{N}\sum -2(y_i - (Wx_i + b)) \end{bmatrix} =\begin{bmatrix} \frac{1}{N}\sum 2x_i(\hat y_i - y_i) \\ \\ \frac{1}{N}\sum 2(\hat y_i - y_i) \end{bmatrix}

Như chúng ta đã biết trong kiến thức giải tích 2 thì chúng ta sẽ đi tìm các điểm local minimum bằng cách giải phương trình đạo hàm bằng 0. Tuy nhiên việc tìm nghiệm này không phải lúc nào cũng đơn giản, hay nói đúng hơn là trong đa số trường hợp là bất khả thi. Nguyên nhân thì có rất nhiều, có thể do số lượng điểm dữ liệu (x,y)(x, y) quá lớn hoặc do việc tính toán đạo hàm quá phức tạp hoặc số chiều của dữ liệu lớn. Điều này khiến chúng ta khó có thể trực tiếp giải phương trình đạo hàm bằng 0 một cách thủ công. Có một phương pháp khá quen thuộc sẽ được áp dụng để giải quyết vấn đề đó. Chúng ta sẽ đi sơ qua ở phần tiếp theo

Giải thuật Gradient Descent

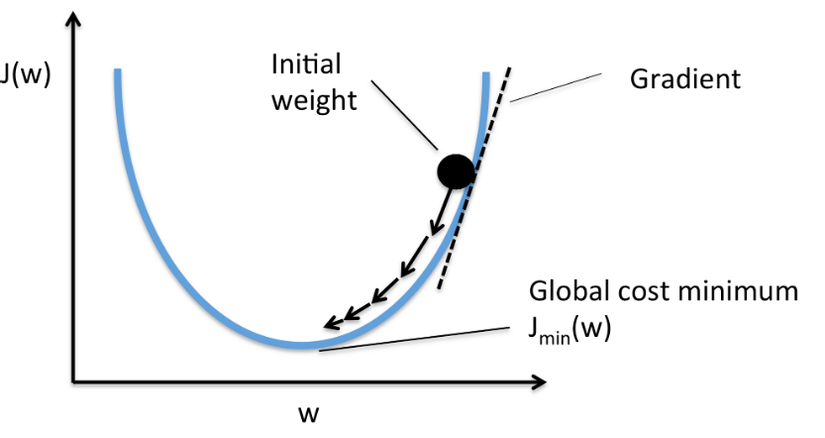
Trong Machine Learning nói chung, việc tìm được các điểm global minimum của hàm số thường là rất khó và gần như là bất khả thi. Thay vì thế người ta thường tìm các điểm local minimum và ở một mức độ chấp nhận được nào đó có thể coi nó như global minimum của bài toán. Để làm được việc đó người ta đưa vào một giải thuật là Gradient Descent chắc hẳn cũng đã khá quen thuộc với khái niệm này trong các bài toán Machine Learning được viết trên Viblo và nhiều blog khác. Mình không giải thích quá sâu về vấn đề này mà chỉ nêu một số tư tưởng chính sau đó chúng ta sẽ tiến hành code luôn. Các bước của GD được mô tả khái quát qua các bước đơn giản như sau:

  • Bước 1: Xuất phát từ một điểm khởi tạo giá trị các trọng số initial weight giả sử là W0W_0
  • Bước 2: Tại bước lặp thứ tt , di chuyển ngược theo dấu của đạo hàm để cập nhật trong số

Wt+1=Wt+ΔW_{t+1} = W_t + \Delta

trong đó Δ\Delta là một đại lương mang dấu ngược với J′(W)J'(W)

  • Bước 3: Thực hiện lặp lại bước 2 cho đến khi J′(W)<ϵJ'(W) < \epsilon thì dừng. Giá trị ϵ\epsilon được chọn sao cho đạo hàm J′(W)≈0J'(W) \approx 0. Lúc này ta coi như tìm được WW sao cho hàm loss JJ đạt giá trị cực tiểu.

Tổng hợp các bước trên, chúng ta có công thực cập nhật đạo hàm đơn giản như sau:

Wt+1=Wt−αJ′(Wt)W_{t+1} = W_t - \alpha J'(W_t)

Trong đó hệ số α\alpha được gọi là tốc độ học hay learning rate và dấu trừ thể hiện việc di chuyển ngược theo hướng của đạo hàm.

Code từ đầu

Cài đặt thuật toán

Chúng ta có thể tóm gọn lại trong đoạn code sau:

import numpy as np
from tqdm import tqdm


class LinearRegression:
    def __init__(self, lr=0.01, epochs=1000):
        self.epochs = epochs
        self.lr = lr
        self.W = 0
        self.b = 0

    def initialize(self, n_features):
        self.W = np.random.normal(0, 1, size=(n_features, 1))
        self.W = np.squeeze(self.W, axis=1)

    def gradient(self, X, y, n_samples):
        y_pred = self.predict(X)
        # Calculate diff
        d_w = (2 / n_samples) * np.dot(X.T, (y_pred - y))
        d_b = (2 / n_samples) * np.sum((y_pred - y))

        return d_w, d_b

    def fit(self, X, y):
        # Load sample and features
        n_samples, n_features = X.shape
        # Init weights
        self.initialize(n_features)
        # Calculate gradient descent per epoch
        for _ in tqdm(range(self.epochs)):
            d_w, d_b = self.gradient(X, y, n_samples)
            self.W -= self.lr * d_w
            self.b -= self.lr * d_b

    def predict(self, X):
        return np.dot(X, self.W) + self.b

Trong đó chúng ta thấy hàm gradient() được triển khai từ công thức trong phần cực tiểu hoá hàm loss

J′(W,b)=[dJdWdJdb]=[1N∑2xi(y^i−yi)1N∑2(y^i−yi)]J'(W, b) = \begin{bmatrix} \frac{dJ}{dW} \\ \\ \frac{dJ}{db} \end{bmatrix} = \begin{bmatrix} \frac{1}{N}\sum 2x_i(\hat y_i - y_i) \\ \\ \frac{1}{N}\sum 2(\hat y_i - y_i) \end{bmatrix}

Trong hàm fit() chúng ta cài đặt giải thuật Gradient Descent lặp lại theo từng epoch đến khi đạt được số lượng epoch nhất định.

Chạy thử

Giờ chúng ta sẽ tiến hành chạy thử với một số tập dữ liệu do chúng ta tự sinh

Khởi tạo dữ liệu

Chúng ta tiến hành khởi tạo tập dữ liệu và phân chia thành 2 phần training và testing

from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression as SkLearnLN
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split


data = make_regression(n_samples=100000, n_features=10)

# Train test split
X_train, X_test, y_train, y_test = train_test_split(data[0], data[1], test_size=0.2)

Khởi tạo mô hình và training

Trong bước này chúng ta sẽ training và so sánh mô hình với thư viện SKLearn

# Fit our model
model = LinearRegression(epochs=2000)
model.fit(X_train, y_train)

# Evaluation our model 
y_pred = model.predict(X_test)
mse = mean_squared_error(y_pred, y_test)

# Fit sklearn model
sklearn_model = SkLearnLN()
sklearn_model.fit(X_train, y_train)

# Evaluation sklearn model 
sk_y_pred = sklearn_model.predict(X_test)
sk_mse = mean_squared_error(sk_y_pred, y_test)

print('Mean square error our: ', mse)
print('Mean square error sklearn: ', sk_mse)

Chúng ta thu được kết quả như sau

100%|██████████| 2000/2000 [00:01<00:00, 1053.16it/s]
Mean square error our:  3.257897561135531e-25
Mean square error sklearn:  1.7868139348369212e-2

Chúng ta có thể thấy được lỗi trên tập test của SKLearn thấp hơn phương pháp của chúng ta một chút nhưng không quá đáng kể. Các bạn cso thể thay đổi tham số như số lượng epoch của thuật toán để thấy được các kết quả khác nhau

Source code

Các bạn có thể tham khảo source code tại đây

Kết luận

Chúng ta đã cùng nhau đi qua bài thứ 2 trong series Machine Learning From Scratch với thuật toán quen thuộc Linear Regression. Kiến thức ở bài này là rất đơn giản và không khó để implement. Hẹn gặp lại các bạn trong các bài tiếp theo
Source: https://viblo.asia/p/ai-from-scratch-basic-ml-2-linear-regression-XL6lADRgZek
Machine Learning