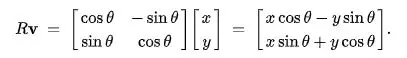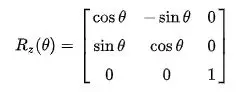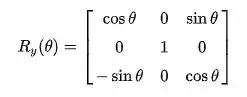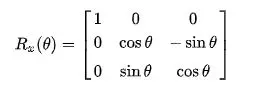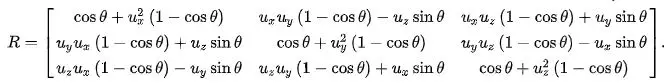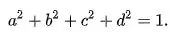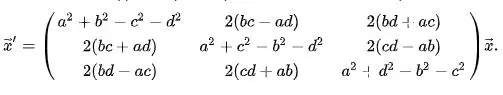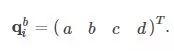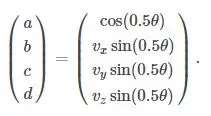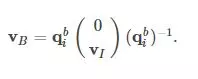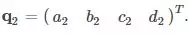Các phương pháp xoay vector trong không gian 2D và 3D

Lời mở đầu

Chào các bạn, mọi người có khỏe không, hôm nay tôi muốn bàn một chút về việc xoay vector trong không gian 2 chiều và 3 chiều. Do không phải dân chuyên Toán nên các thuật ngữ như Euler, Quaternions, ... tôi cũng chả có cách nào giải thích cho các bạn, nhưng đưa ra vài ví dụ trong lập trình chắc vẫn được nên hôm nay tôi viết bài này cũng muốn tham khảo ý kiến một chút.

Xoay vector trong không gian 2D

Như các bạn đã biết, không gian 2D chỉ chứa trục x và trục y nên ta nhìn qua là một mặt phẳng không có chiều sâu. Để rõ ràng, tôi sẽ minh họa một vector tạo thành từ 2 điểm bất kỳ bằng thư viện matplotlib.

from matplotlib import pyplot as plt
import math
import numpy as np

p1 = [0, 0]
p2 = [40, 40]

plt.axis([-50, 50, -50, 50])
plt.plot([p1[0], p2[0]], [p1[1], p2[1]], label = "line 1")

Tôi đã có 1 vector trong không gian 2 chiều, giờ tôi sẽ xoay vector theo một góc chỉ định, ở đây tôi lấy góc 90 độ. Dựa trên công thức dưới đây sẽ sinh ra x y của vector mới

Nếu code theo python thì ta có

newX = v[0] * math.cos(angle) - v[1] * math.sin(angle)
newY = v[0] * math.sin(angle) + v[1] * math.cos(angle)

Nhưng như thế vector sẽ bị xoay ngược chiều kim đồng hồ nên tôi phải thay đổi một chút

newX = v[0] * math.cos(angle) + v[1] * math.sin(angle)
newY = -v[0] * math.sin(angle) + v[1] * math.cos(angle)

Minh họa dựa theo matplotlib

p1 = [0, 0]
p2 = [40, 40]

plt.axis([-50, 50, -50, 50])
plt.plot([p1[0], p2[0]], [p1[1], p2[1]], label = "line 1")

v = [p2[0] - p1[0], p2[1] - p1[1]]

angle = np.deg2rad(90)

newX = v[0] * math.cos(angle) + v[1] * math.sin(angle)
newY = -v[0] * math.sin(angle) + v[1] * math.cos(angle)

p3 = [p1[0] + newX, p1[1] + newY]

plt.axis([-50, 50, -50, 50])
plt.plot([p1[0], p3[0]], [p1[1], p3[1]], label = "line 2")

plt.xlabel('x')
plt.ylabel('y')
plt.show()

Xoay vector bởi 180 độ

Xoay vector trong không gian 3D

Không gian bao gồm chiều rộng x, chiều cao y và chiều sâu z. Một điểm nằm trong không gian này có giá trị (x, y, z). Cũng như việc xoay vector trong không gian 2 chiều, tôi cần tìm ma trận rotation R rồi nhân với tọa độ của vector sẽ sinh ra một vector mới.

Xoay vector theo trục

Cho một góc 90 độ, chuyển từ độ (degree) thành radian, chọn trục z làm trục quay, tìm rotation vector của trục quay bằng thư viện scipy. Tôi giải thích sơ qua module Rotation của thư viện này chút.

Đầu tiên tìm unit vector của trục (axis)
Sau đó cross product của unit vector với ma trận I (Identify matrix).
Cuối cùng dùng hàm exponential với param là góc và A sẽ trả về ma trận xoay (rotation matrix)

a = axis/norm(axis) #1
A = I x a
exp(theta,A)

Sau khi có ma trận xoay chỉ cần nhân với vector cần xoay sẽ sinh ra một vector mới quay theo trục một góc 90 độ.

from scipy.spatial.transform import Rotation as R

vec = [1,1,1]

rotation_degrees = 90
rotation_radians = np.radians(rotation_degrees)
rotation_axis = np.array([0, 0, 1])

rotation_vector = rotation_radians * rotation_axis
rotation = R.from_rotvec(rotation_vector)
rotated_vec = rotation.apply(vec)

print(rotated_vec)

Euler angle

Định nghĩa: miêu tả hướng của một vật thể trong không gian 3 chiều

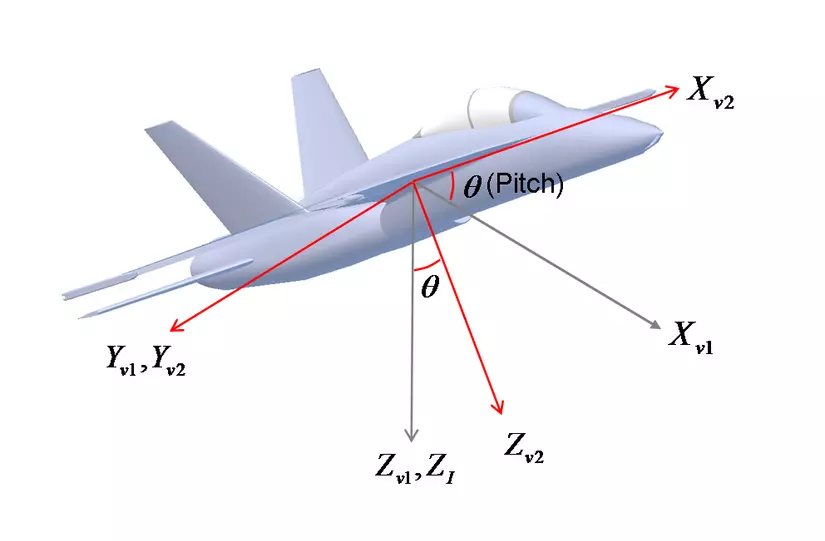
Ví dụ: Giả sử tôi có một video quay một máy bay, khi xử lý video cung cấp các frame và tọa độ x y z. Ở frame đầu tiên, máy bay được coi là không dịch chuyển. Từ frame thứ 10 máy bay dịch chuyển và thay đổi vị trí một góc 30 độ. Quá trình biến đổi hướng có thể chia thành 3 giai đoạn:

Yaw Rotation: chuyển động quay quanh trục z của vector một góc ψ, tạo nên tọa độ mới mà trục z không thay đổi nhưng trục x, y quay theo góc ψ.

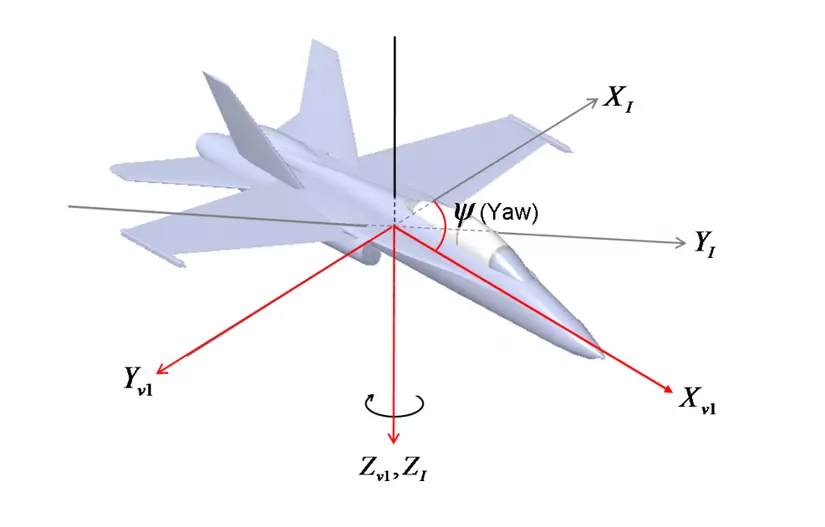
Pitch Rotation

Roll Rotation

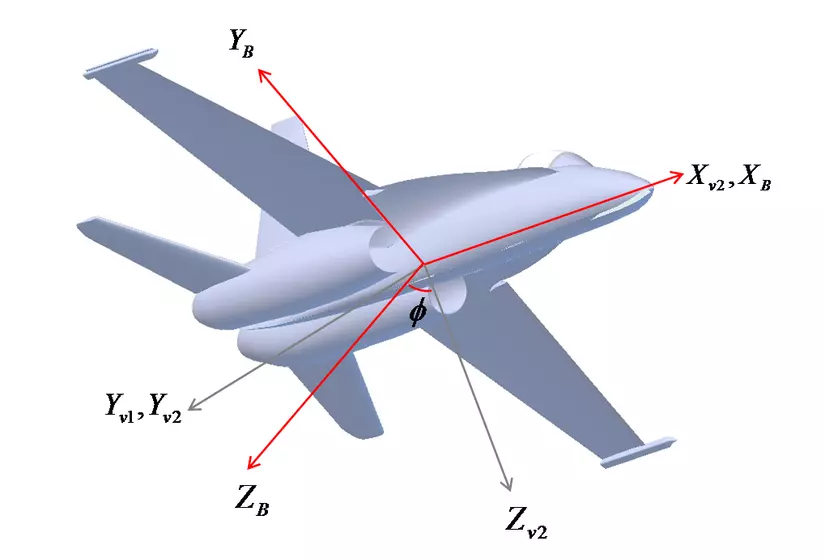
Ma trận xoay theo góc và trục chỉ định (ux, uy, uz). Với u là unit vector

from math import pi ,sin, cos

def R(theta, u):
    return [[cos(theta) + u[0]**2 * (1-cos(theta)), 
             u[0] * u[1] * (1-cos(theta)) - u[2] * sin(theta), 
             u[0] * u[2] * (1 - cos(theta)) + u[1] * sin(theta)],
            [u[0] * u[1] * (1-cos(theta)) + u[2] * sin(theta),
             cos(theta) + u[1]**2 * (1-cos(theta)),
             u[1] * u[2] * (1 - cos(theta)) - u[0] * sin(theta)],
            [u[0] * u[2] * (1-cos(theta)) - u[1] * sin(theta),
             u[1] * u[2] * (1-cos(theta)) + u[0] * sin(theta),
             cos(theta) + u[2]**2 * (1-cos(theta))]]

def Rotate(pointToRotate, point1, point2, theta):
    u= []
    squaredSum = 0
    for i,f in zip(point1, point2):
        u.append(f-i)
        squaredSum += (f-i) **2

    u = [i/squaredSum for i in u]

    r = R(theta, u)
    rotated = []

    for i in range(3):
        rotated.append(round(sum([r[j][i] * pointToRotate[j] for j in range(3)])))

    return rotated

point = [1,0,0]
p1 = [0,0,0]
p2 = [0,1,0]

print Rotate(point, p1, p2, pi)

Công thức Euler–Rodrigues

Định nghĩa: một phương pháp tính vị trí của rotated point.

Một phép xoay quanh trục tọa độ gốc được biểu diễn bởi 4 param a, b, c, d

Khi áp dụng công thức này, một điểm có tọa độ x sẽ xoay về một vị trí mới có tọa độ x'

Code python: hàm rotation_matrix() trả về một ma trận xoay ngược chiều kim đồng hồ theo trục và góc.

import numpy as np
import math

def rotation_matrix(axis, theta):
    """
    Return the rotation matrix associated with counterclockwise rotation about
    the given axis by theta radians.
    """
    axis = np.asarray(axis)
    axis = axis / math.sqrt(np.dot(axis, axis))
    a = math.cos(theta / 2.0)
    b, c, d = -axis * math.sin(theta / 2.0) # bỏ dấu trừ nếu muốn thuận chiều kim đồng hồ
    aa, bb, cc, dd = a * a, b * b, c * c, d * d
    bc, ad, ac, ab, bd, cd = b * c, a * d, a * c, a * b, b * d, c * d
    return np.array([[aa + bb - cc - dd, 2 * (bc + ad), 2 * (bd - ac)],
                     [2 * (bc - ad), aa + cc - bb - dd, 2 * (cd + ab)],
                     [2 * (bd + ac), 2 * (cd - ab), aa + dd - bb - cc]])

v = [3, 5, 0]
axis = [4, 4, 1]
theta = 1.2 

print(np.dot(rotation_matrix(axis, theta), v)) 
# [ 2.74911638  4.77180932  1.91629719]

Quaternions

Cũng như Euler-Rodrigues, quaternion là một vector có 4 phần tử dùng để tính vị trí của rotated point. Ta cũng có thể biến đổi Euler parameters a, b, c, d trên thành các hệ số của quaternion

Một quaternion có thể tính như sau

def angle_axis_quat(theta, axis):
    """
    Given an angle and an axis, it returns a quaternion.
    """
    axis = np.array(axis) / np.linalg.norm(axis)
    return np.append([np.cos(theta/2)],np.sin(theta/2) * axis)

Xoay vector bởi quaternions bằng công thức

Một vector xoay là tích của một quaternion với nghịch đảo của nó. Quaternion này lại là tích của unit vector với liên hợp của nó.

q1:

q2:

Tích của 2 quaternions

def mult_quat(q1, q2):
    """
    Quaternion multiplication.
    """
    q3 = np.copy(q1)
    q3[0] = q1[0]*q2[0] - q1[1]*q2[1] - q1[2]*q2[2] - q1[3]*q2[3]
    q3[1] = q1[0]*q2[1] + q1[1]*q2[0] + q1[2]*q2[3] - q1[3]*q2[2]
    q3[2] = q1[0]*q2[2] - q1[1]*q2[3] + q1[2]*q2[0] + q1[3]*q2[1]
    q3[3] = q1[0]*q2[3] + q1[1]*q2[2] - q1[2]*q2[1] + q1[3]*q2[0]
    return q3

Sau khi có được rotated quaternions, áp dụng vào vector cần xoay sẽ sinh ra một vector mới.

def rotate_quat(quat, vect):
    """
    Rotate a vector with the rotation defined by a quaternion.
    """
    # Transfrom vect into an quaternion 
    vect = np.append([0],vect)
    # Normalize it
    norm_vect = np.linalg.norm(vect)
    vect = vect/norm_vect
    # Computes the conjugate of quat
    quat_ = np.append(quat[0],-quat[1:])
    # The result is given by: quat * vect * quat_
    res = mult_quat(quat, mult_quat(vect,quat_)) * norm_vect
    return res[1:]

v = [3, 5, 0]
axis = [4, 4, 1]
theta = 1.2 

print(rotate_quat(angle_axis_quat(theta, axis), v))
# [2.74911638 4.77180932 1.91629719]

Lời kết

Như các bạn thấy thì cả bài này hầu như là một bài tổng hợp các cách xoay vector trong không gian hai chiều và ba chiều, do đó còn nhiều thiếu sót và không đầy đủ, mong các cao nhân có thể giúp đỡ thêm thắt lý thuyết công thức cho tác giả và người đọc hiểu thêm.