Introduction

Bài toán face recognition trong vài năm trở lại đây đã đạt dược nhiều bước tiến lớn nhờ vào sự phát triển của học sâu (Deep learning), mà cụ thể hơn là mạng neural tích chập (Convolutional neural network - CNN). Các phương pháp deep learning based hầu hết dựa vào mạng CNN để trích xuất ra một vector đặc trưng đại diện cho một khuôn mặt gọi là vector face embedding. Các vector này có đặc điểm là nếu 2 vector được trích xuất từ 2 bức ảnh của cùng 1 người thì khoảng cách giữa chúng sẽ nhỏ (small intra-class distance). Ngược lại, nếu 2 vector từ 2 ảnh của 2 người thì khoảng cách sẽ lớn (large inter-class distance). Hiện nay có 2 xu hướng nghiên cứu chủ đạo để huấn luyện CNN cho face recognition

• Coi face recognition là 1 bài toán phân lớp thông thường và áp dụng hàm kích hoạt softmax và cross entropy loss để mô hình học được xác suất 1 khuôn mặt sẽ thuộc vào lớp nào. Sau đó vector face embedding được trích xuất từ output của 1 lớp fully connected trong mạng.
• Hướng thứ 2 là cho mạng học trực tiếp vector face embedding sử dụng contrastive loss và triplet loss. Điển hình cho hướng này thì có mô hình Facenet rất nổi tiếng.

Trong bài viết này, mình sẽ tìm hiểu về một số phương pháp để cải thiện hàm mất mát.

Categorical Cross-Entropy loss

Hay còn được gọi là Softmax loss. Đây là hàm loss thông dụng nhất được sử dụng cho bài toán multi-class classification. Bao gồm hàm kích hoạt softmax tác động vào output của lớp fully connected cuối cùng của mạng (logit) và cross-entropy loss:

$L_i = -\frac{1}{N}\sum^{N}_{i=1}log\frac{e^{W_{y_i}^Tx_i + b_{y_i}}}{e^{\sum^n_{j=1}W_{j}^Tx_i + b_{j}}}$

Trong phương trình trên, $x_i$ là vector thuộc $\mathbb{R}^d$; $W_j\in \mathbb{R}^d$ là cột thứ j của ma trận trọng số $W\in\mathbb{R}^{d\times n}$; N và n lần lượt là batch size và số class trong tập dữ liệu. Softmax loss có nhược điểm là nó không trực tiếp tối ưu vector face embedding để đạt được khoảng cách nhỏ giữa các vector trong cùng 1class và khoảng cách lớn khi khác class. # Large Margin Softmax Paper [Large-Margin Softmax Loss for Convolutional Neural Networks](https://arxiv.org/pdf/1612.02295.pdf) là một trong những paper đầu tiên giới thiệu khái niệm về margin (lề) vào softmax loss. Margin ở đây được sử dụng để tăng inter-class distance giữa các class và đồng thời làm giảm intra-class distance. Softmax loss được biến đổi lại như sau $$f_j =W^T_jx_i

Dễ thấy, công thức trên là tích vô hướng giữa $W_j$ và $x_i$. Như đã được học trong môn đại số, tích vô hướng có thể được viết lại thành:

$f_j =W^T_jx_i =||W_j||||x_i||cos(\theta_j)$

trong đó, $\theta_i$ là góc giữa 2 vector $W_j$ và $x_i$. Trong phân lớp nhị phân sử dụng softmax los, một ảnh sẽ được phân vào lớp thứ nhất nếu $W_1^Tx > W_2^Tx$ hoặc $||W_1||||x|| cos(θ_1) > ||W_2||||x|| cos(θ_2)$. Nhưng ta cần 1 khoảng margin m giữa decision boundary của 2 class nên, tác giả paper yêu cầu $||W_1||||x|| cos(θ_1) > ||W_2||||x|| cos(θ_2) (0 \leq\theta_1\leq \frac{\pi}{m})$. Desion boundary từ đó sẽ trở thành

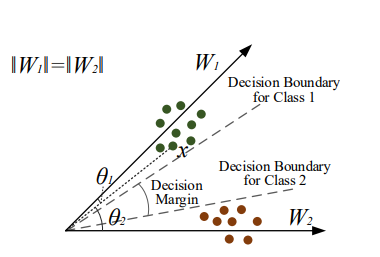
Hàm L-softmax loss được định nghĩa là

$L_i = -log\frac{e^{||W_{y_i}||||x_i||\psi(\theta_{y_i})}}{e^{||W_{y_i}||||x_i||\psi(\theta_{y_i})+\sum_{j\neq y_i}||W_{y_i}||||x_i||cos(\theta_{j})}}$

$\psi(\theta)= \begin{cases} cos(m\theta), 0\leq \theta \leq \frac{\pi}{m}\ \\ D(\theta), \frac{\pi}{m} \leq \theta \leq \pi\\ \end{cases}$

trong đó m là 1 số thực dương. m càng lớn thì margin sẽ càng lớn. $D(\theta)$ là 1 hàm đơn điệu giảm sao cho $D( \frac{\pi}{m}) = cos( \frac{\pi}{m})$ Hàm $\psi$ được xây dựng trong paper:

$\psi(\theta) = (-1)^kcos(m\theta), \theta \in [ \frac{k\pi}{m}, \frac{(k+1)\pi}{m}], k\in [0, m-1]$

Angular Softmax (A-Softmax)

Về mặt công thức, Angular softmax giống hệt như L-softmax. Điểm khác biệt duy nhất là trong A-softmax sẽ chuẩn hóa vector $W_i$ sao cho $||W_i||=1$. Hàm L-softmax sẽ trở thành

$L_i = -log\frac{e^{||x_i||\psi(\theta_{y_i})}}{e^{||x_i||\psi(\theta_{y_i})+\sum_{j\neq y_i}||x_i||cos(\theta_{j})}}$

A-softmax không chỉ làm tăng tính phân biệt cho các vector embedding mà còn có một số đặc tính hình học khá thú vị

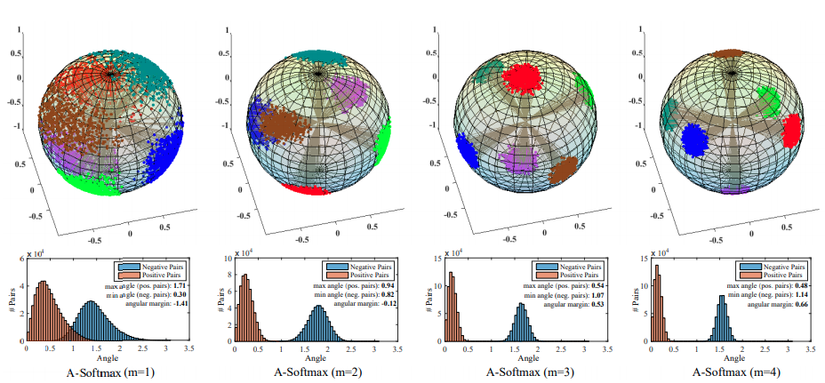
Phía trên là hình ảnh trực quan của các các vector face embedding đã được học với các giá trị m khác nhau. Hàng đầu tiên hiển thị các vector 3D được chiếu trên hình cầu đơn vị. Các điểm màu là giao điểm của vector embedding và hình cầu đơn vị. Hàng thứ hai hiển thị sự phân bố góc của cả cặp dương tính và cặp âm tính (tác giả chọn lớp 1 và lớp 2 từ tập con của dataset CASIA-WebFace để xây dựng các cặp ảnh âm tính và dương tính ). Vùng màu cam biểu thị các cặp dương tính trong khi màu xanh lam biểu thị các cặp âm tính . Giá trị các góc được tính bằng radian.

Additive Angular Margin Softmax

Paper ArcFace: Additive Angular Margin Loss for Deep Face Recognition có cách tiếp cận khác để giới thiệu margin cho decision boundary. Thay vì nhân m với $\theta$ như trong L-softmax và A-softmax, tác giả thay đổi hàm $\psi(\theta)$ thành

$\psi(\theta) = cos(\theta + m)$

Công thức này đơn giản hơn rất nhiều so với $\psi(\theta)$ của L-Softmax và A-Softmax và Arcface cũng hoạt động tốt hơn. Bên cạnh đó, Arcface cũng chuẩn hóa cũng chuẩn hóa trọng số $W_i$ giống với A-softmax và đồng thời cũng chuẩn hóa cả vector embedding $x_i$ sao cho $||x_i|| = s$ (s là 1 hyperparameter) Cuối cùng, loss của Arcface có thể được xác định như sau:

$L_i = -log\frac{e^{s\cos(\theta_{y_i} + m)}}{e^{s\cos(\theta_{y_i}+m)+\sum_{j\neq y_i}scos(\theta_{j})}}$

Thuật toán của arcface:

1. Chuẩn xóa vector $||x||$ và các cột của ma trận trọng số $W$
2. Tính $Wx$
3. Tính $cos(\theta_j)$ giữa từng cột của ma trận $W$ và $x$
4. Tính $arccos(\theta_j)$ giữa từng cột của ma trận $W$ và $x$
5. Cộng $\theta$ của class groudn truth với margin m (góc tính bằng radian)
6. Nhân giá trị logit với $||x_i||$
7. Tính softmax loss như trong công thức

Tổng kết

Trên đây, mình đã giới thiệu một số cải tiến của cross-entropy loss để tăng hiệu suất của mô hình deep learning trong bài toán face recognition nói riêng và classification nói riêng. Bài viết tới đây là hết. Cảm ơn mọi người đã theo dõi.