Skip to content

Dashboard

Thuật Toán Insertion Sort Đơn Giản

Created by Admin

1. Overview (Tổng Quan)

Tiếp tục SERI Thuật Toán Sắp Xếp Đơn Giản chúng ta sẽ tìm hiểu một thuật toán rất dễ để cài đặt mà bất kì bạn sinh viên nào cũng sẽ được học ngay từ những năm đầu tiên của đại học. Giới thiệu qua cho bạn nào chưa biết : SERI Thuật Toán Đơn Giản chúng ta sẽ tìm hiểu những thuật toán bao gồm Bubble Sort, Insertion Sort, Merge Sort, Heap Sort, QuickSort, Radix Sort, Counting Sort, Bucket Sort, ShellSort . Trong bài viết này mình chúng ta sẽ tìm hiểu về Insertion Sort .

2. Insertion Sort (Sắp Xếp Chèn)

Sắp xếp chèn là một thuật toán sắp xếp đơn giản hoạt động tương tự như cách bạn sắp xếp các thẻ chơi trong tay của mình. Mảng hầu như được chia thành một phần được sắp xếp và một phần chưa được sắp xếp. Các giá trị từ phần chưa được sắp xếp được chọn và đặt ở vị trí chính xác trong phần được sắp xếp.

Thuật toán

Để sắp xếp một mảng có kích thước n theo thứ tự tăng dần:

1: Lặp lại từ arr [1] đến arr [n] trên mảng.

2: So sánh phần tử hiện tại (khóa) với phần tử tiền nhiệm của nó.

3: Nếu phần tử chính nhỏ hơn phần tử trước của nó, hãy so sánh nó với các phần tử trước đó. Di chuyển các phần tử lớn hơn lên một vị trí để tạo khoảng trống cho phần tử được hoán đổi.

Dưới đây là một ví dụ: Đầu vào là một mảng 12, 11, 13, 5, 6 chưa được sắp xếp.

def insertionSort(arr):
 
    for i in range(1, len(arr)):
 
        key = arr[i]
        
        # Di chuyển các phần tử của mảng arr[0..i-1], lớn hơn key, 
        # đến một vị trí phía trước vị trí hiện tại
        j = i-1
        while j >= 0 and key < arr[j] :
                arr[j + 1] = arr[j]
                j -= 1
        arr[j + 1] = key
 
 
# Kết Quả
arr = [12, 11, 13, 5, 6]
insertionSort(arr)
for i in range(len(arr)):
    print ("% d" % arr[i])

Giải thích cho đoạn code trên

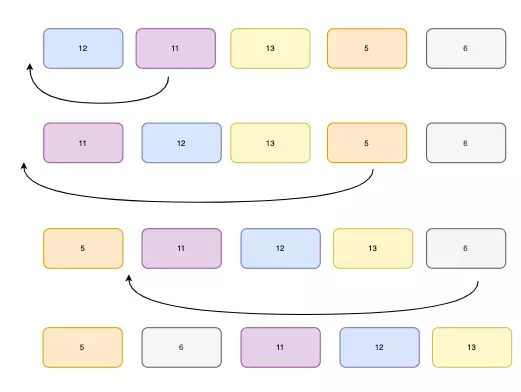
**12, 11, 13, 5, 6
bắt đầu vòng for i = 1 (phần tử thứ 2 array) to 4 (phần tử cuối cùng của array)
i = 1. thấy 11 nhỏ hơn 12, di chuyển 12 và chèn 11 trước 12 
**11, **12 13, 5, 6
i = 2. 13 sẽ vẫn giữ vị trí của nó vì tất cả phần tử từ A[0..I-1] đều nhỏ hơn 13
**11, **12, **13, 5, 6
i = 3. 5 sẽ di chuyển về đầu tiên và tất cả các phần tử từ 11 đến 13 di chuyển về phái sau 1 chỉ số. 
**5, **11, **12, **13, 6
i = 4. 6 sẽ chạy về sau 5, và tất cả các phần tử từ 11 đến 13 di chuyển về phái sau 1 chỉ số . 
**5, **6, **11, **12, **13

Dưới đây là sơ đồ khối giải thích cho đoạn code trên

Thuật toán Insertion Sort có độ phức tạp là O(n^2) vì có 2 vòng lặp lồng nhau.

3. Conclusion (Kết Luận)

Thông qua bài viết này chúng ta đã tìm hiểu về thuật toán Insertion Sort . Các thành phần của Insertion Sort. Độ phúc tạp của thuật toán và cách cài đặt thuật toán thông qua ví dụ. Rất mong đã đem lại những kiến thức thú vị cho các bạn. Nếu thấy hữu ích các bạn nhớ bấm follow mình nha.!! Bài Viết Cùng Seri:
Source: https://viblo.asia/p/thuat-toan-insertion-sort-don-gian-bWrZnVapZxw
Algorithm May Fest datastructures