Ở bài viết này, mình sẽ không thảo luận về lý thuyết của tiêu chuẩn mã hóa dữ liệu (Data Encryption Standard - DES), hay cụ thể là Simplified DES. Thay vào đó, mình sẽ thực hành mã hóa bằng tay từng bước thuật toán Simplified DES và thực hiện giải mã thông qua công cụ SageMath để kiểm tra xem có đúng Plaintext trước đó hay không.

Cùng bắt tay thực hiện nào!

Task 1: Thực hiện mã hóa Simplified DES (Encryption) bằng tay để tìm ciphertext

Mình sẽ sử dụng các chữ cái đầu của chữ lót và tên cá nhân để phục vụ cho việc khởi tạo input, cụ thể như sau:

Tên: Minh Khanh

M = 4d = 0100 1101, lấy đây là giá trị Plaintext 8 bits

K = 4b = 0100 1011, thêm 10 vào sau làm giá trị Key 10 bits

Vậy, input của mình bao gồm:

• Plaintext = 0100 1101
• Key = 0100 1011 10

1.1. Initial permutation

Đánh thứ tự các bits của plaintext:

b0	b1	b2	b3	b4	b5	b6	b7
0	1	0	0	1	1	0	1

Hoán vị theo quy tắc sau:

(b0, b1, b2, b3, b4, b5, b6, b7) → (b1, b5, b2, b0, b3, b7, b4, b6)

b1	b5	b2	b0	b3	b7	b4	b6
1	1	0	0	0	1	1	0

Vậy, initial permutation = 1100 0110

1.2. Subkeys

Đánh thứ tự các bits của key:

b0	b1	b2	b3	b4	b5	b6	b7	b8	b9
0	1	0	0	1	0	1	1	1	0

a. Đầu tiên, 10 bits của key sẽ được hoán vị theo quy tắc:

(b0, b1, b2, b3, b4, b5, b6, b7, b8, b9) → (b2, b4, b1, b6, b3, b9, b0, b8, b7, b5)

b2	b4	b1	b6	b3	b9	b0	b8	b7	b5
0	1	1	1	0	0	0	1	1	0

b. Chia làm hai nửa, mỗi bên 5 bits: (0, 1, 1, 1, 0), (0, 0, 1, 1, 0)

c. Với lượt 1, mỗi bên sẽ dịch 1 bit sang trái theo vòng theo quy luật:

(a, b, c, d, e), (f, g, h, i, j) → (b, c, d, e, a), (g, h, i, j, f)

Ta được,

(0, 1, 1, 1, 0), (0, 0, 1, 1, 0) → (1, 1, 1, 0, 0), (0, 1, 1, 0, 0)

b0	b1	b2	b3	b4	b5	b6	b7	b8	b9
1	1	1	0	0	0	1	1	0	0

d. Ta được subkey đầu tiên bằng cách lấy các bit ở vị trí (5, 2, 6, 3, 7, 4, 9, 8) là K1 = 01101000

e. Với lượt 2, kết quả của bước 3 sẽ được dịch 2 bits sang trái:

(b, c, d, e, a), (g, h, i, j, f) → (d, e, a, b, c), (i, j, f, g, h)

Ta được,

(1, 1, 1, 0, 0), (0, 1, 1, 0, 0) → (1, 0, 0, 1, 1), (1, 0, 0, 0, 1)

b0	b1	b2	b3	b4	b5	b6	b7	b8	b9
1	0	0	1	1	1	0	0	0	1

Ta được subkey 2 bằng cách lấy các bits ở các vị trí tương tự như subkey 1: K2 = 10010110

Quy tắc:

Nếu key là k0 k1 k2 k3 k4 k5 k6 k7 k8 k9 thì 2 subkey sẽ là:

• K1 = k0 k6 k8 k3 k7 k2 k9 k5
• K2 = k7 k2 k5 k4 k9 k1 k8 k0

The Feistel step

1. Initial permutation = 11000110
2. Chia làm 2 nửa, nửa bên phải là 0110 được mix với subkey K1.

Trước tiên, 4 bits 0110 được mở rộng thành 8 bits theo quy tắc sau:

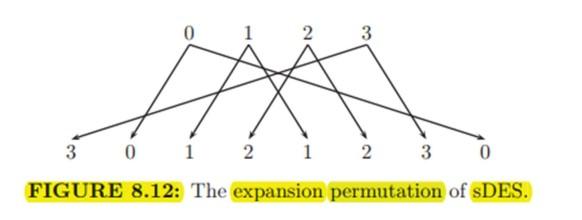
Hay b0 b1 b2 b3 → b3 b0 b1 b2 b1 b2 b3 b0

Ta được kết quả là: 0 1 1 0 → 0 0 1 1 1 1 0 0

Sau đó mang 8 bits này XOR với K1:

	0	0	1	1	1	1	0	0
⊕	0	1	1	0	1	0	0	0
=	0	1	0	1	0	1	0	0

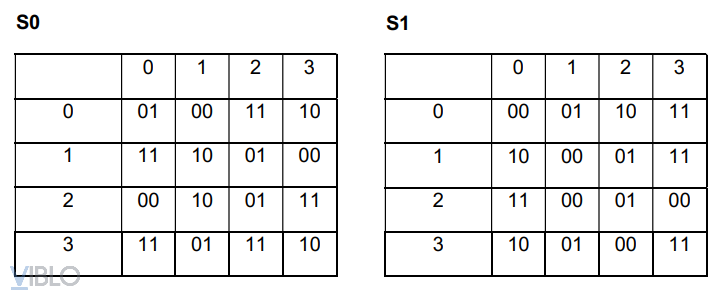
4 bits đầu tiên 0101 được dùng làm input cho S0, và 4 bits tiếp theo 0100 được dùng làm input cho S1:

• 2 bits ngoài cùng là 01 dùng làm hàng, tức là hàng thứ 1, 2 bits trong cùng là 10 dùng làm cột, tức là cột thứ 2. Lấy giá trị ở hàng 1 cột 2 của bảng S0 ta được 01.

• 2 bits ngoài cùng là 00 dùng làm hàng, tức là hàng thứ 0, 2 bits trong cùng là 10 dùng làm cột, tức là cột thứ 2. Lấy giá trị ở hàng 0 cột 2 của bảng S1 ta được 10.

Kết hợp lại ta được 0110

Permuted:

Công thức: (b0, b1, b2, b3) → (b1, b3, b2, b0)

Suy ra, kết quả permuted là 1010

Kết quả này XOR với nửa bên trái:

1010 ⊕ 1100 = 0110 và ghép với nửa bên phải 0110 tạo thành 0110 0110

3. Đảo vị trí 2 nửa: 0110 0110
4. Nửa trái hiện tại là 0110 và nửa phải là 0110, với K2 = 10010110.

Mở rộng nửa bên phải: 0 1 1 0 → 0 0 1 1 1 1 0 0

XOR với K2:

	0	0	1	1	1	1	0	0
⊕	1	0	0	1	0	1	1	0
=	1	0	1	0	1	0	1	0

Đặt 2 nửa 1010 và 1010 vào S0 và S1 như trên ta được:

• 2 bits ngoài cùng là 10 dùng làm hàng, tức là hàng thứ 2, 2 bits trong cùng là 01 dùng làm cột, tức là cột thứ 1. Lấy giá trị ở hàng 2 cột 1 của bảng S0 ta được 10

• 2 bits ngoài cùng là 10 dùng làm hàng, tức là hàng thứ 2, 2 bits trong cùng là 01 dùng làm cột, tức là cột thứ 1. Lấy giá trị ở hàng 2 cột 1 của bảng S1 ta được 00

Kết hợp lại ta được 1000

Theo công thức phía trên, kết quả permuted là 0001

Kết quả này XOR với nửa bên trái:

0001 ⊕ 0110 = 0111 và ghép với nửa bên phải 0110 tạo thành 0111 0110

5. Hoán vị đảo cuối cùng: 0111 0110 → 1010 1101

Vậy,

ciphertext = 1010 1101

Task 2: Thực hiện mã hóa và giải mã Simplified DES (Decryption) để tìm ngược lại Plaintext thông qua công cụ SageMath

a. Thực hiện mã hóa plaintext với P và K lấy từ bài 1:

• P = 0100 1101
• K = 0100 1011 10

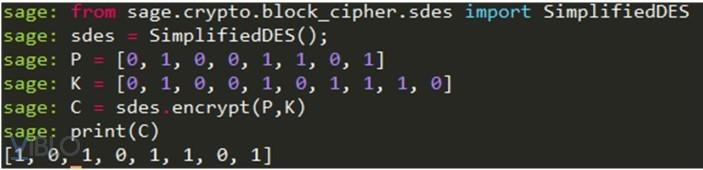
Kết quả ciphertext khi chạy trên Sage hoàn toàn trùng khớp với kết quả mà mình đã thực hành bằng tay ở Task 1.

b. Thực hiện giải mã ciphertext với C lấy từ kết quả trên:

• C = 1010 1101

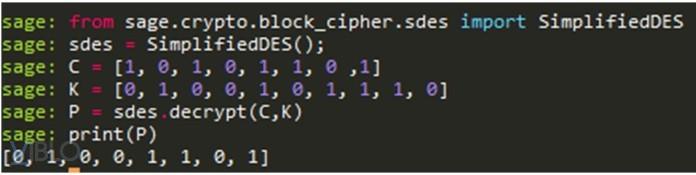
Kết quả plaintext khi chạy trên Sage hoàn toàn trùng khớp với Plaintext ban đầu.