Tương tự bài viết trước về thuật toán Simplified AES, mình sẽ không thảo luận về lý thuyết của tiêu chuẩn mã hóa dữ liệu Advanced Encryption Standard - AES, hay cụ thể là Simplified AES. Thay vào đó, mình sẽ thực hành mã hóa và giải mã bằng tay từng bước thuật toán Simplified AES.

Cùng bắt tay thực hiện nào!

Task 1: Thực hiện mã hóa Simplified AES (Encryption) bằng tay để tìm ciphertext

Mình sẽ sử dụng các chữ cái đầu trong tên cá nhân để phục vụ cho việc khởi tạo input, cụ thể như sau:

Tên: Chau Minh Khanh

C = 43 = 0100 0011

M = 4D = 0100 1101

K = 5B = 0100 1011

Tạo Plaintext (16 bits) từ 2 chữ cái đầu của họ và tên:

Plaintext = CK = 0100 0011 0100 1011

Tạo Key (16 bits) từ 2 chữ cái đầu của chữ lót và tên:

Key = MK = 0100 1101 0100 1011

1.1. Key Generation:

Ở bước đầu tiên, ta sẽ tạo ra các sub-key. Quá trình này gọi là Key Generation.

Ta chia key đã tạo phía trên thành 2 phần, gọi là w0 và w1:

w0 = 0100 1101

w1 = 0100 1011

Sub-key đầu tiên cũng chính là key ban đầu, tức là:

Key0 = w0w1 = K

Các sub-key còn lại được tạo như sau:

w2 = w0 XOR 10000000 XOR SubNib(RotNib(w1))

Trong đó, RotNib() là hàm để đảo vị trí 4 bit đầu và 4 bit cuối với nhau, cụ thể

RotNib(w1) = RotNib(0100 1011) = 1011 0100

Suy ra,

w2 = 0100 1101 XOR 10000000 XOR SubNib(1011 0100)

Ta dùng bảng sau để tra cứu output của hàm SubNib():

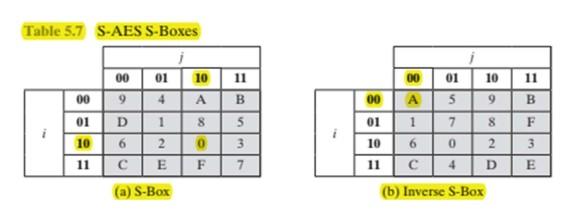
Theo đó,

w2 = 0100 1101 XOR 10000000 XOR SubNib(1011 0100) = 1100 1101 XOR 0011 1101 = 1111 0000

w3 = w2 XOR w1 = 1111 0000 XOR 0100 1011 = 1011 1011

w4 = w2 XOR 0011 0000 XOR SubNib(RotNib(w3)) 
= 1111 0000 XOR 0011 0000 XOR SubNib(1011 1011)
= 1100 0000 XOR 0011 0011
= 1111 0011

w5 = w4 XOR w3 = 1111 0011 XOR 1011 1011 = 0100 1000

Các sub-key sẽ là:

Key0 = w0w1 = 0100 1101 0100 1011

Key1 = w2w3 = 1111 0000 1011 1011

Key2 = w4w5 = 1111 0011 0100 1000

1.2. Encryption:

Ta sẽ thực hiện quá trình thêm các key theo từng vòng.

1.2.1. Add Round 0 Key:

Plaintext XOR Key0 = 0100 0011 0100 1011 XOR 0100 1101 0100 1011 = 0000 1110 0000 0000

1.2.2. Round 1:

Sử dụng S-box phía trên với input là kết quả của phép XOR vừa thực hiện:

Input = 0000 1110 0000 0000

Output = 1001 1111 1001 1001

Shift Row. Hoán vị trí nibble thứ 2 và 4 với nhau = 1001 1001 1001 1111

Mix Columns. Áp dụng phép nhân ma trận với ma trận hằng M

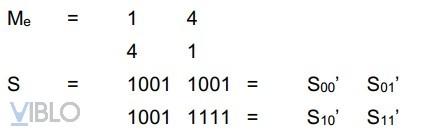
với S’ = Me x S

Ta có:

S00’ = S00 XOR (4 x S10)
= 1001 XOR (4 x 1001)
= 1001 XOR (4 x 9) (row 4 col 9)
= 1001 XOR 2 = 1001 XOR 0010 = 1011

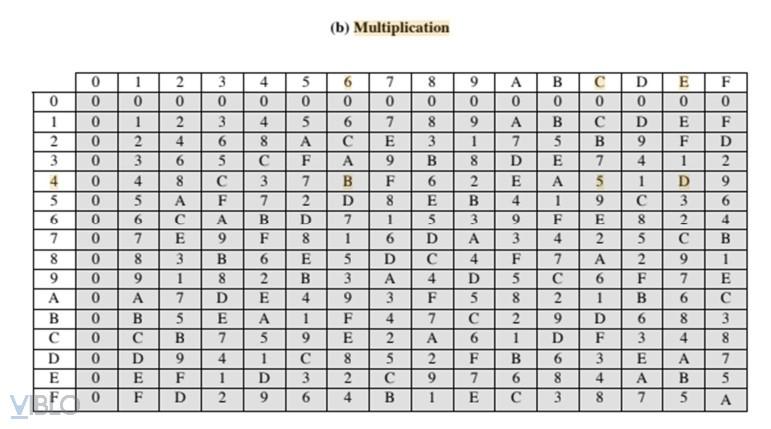
S10’ = (4 x S00) XOR S10 = (4 x 1001) XOR 1001 = 0010 XOR 1001 = 1011

S01’ = S01 XOR (4 x S11) = 1001 XOR (4 x 1111) = 1001 XOR (4 x F) =
= 1001 XOR 9 = 1001 XOR 1001 = 0000

S11’ = (4 x S01) XOR S11 = (4 x 1001) XOR 1111 = 0010 XOR 1111 = 1101

Ta được:

Output = S00’S10’S01’S11’ = 1011 1011 0000 1101

Add Round 1 Key

= 1011 1011 0000 1101 XOR Key1 
= 1011 1011 0000 1101 XOR 1111 0000 1011 1011
= 0100 1011 1011 0110

1.2.3. Final Round

Lấy kết quả ở Round trên làm input, tra cứu bảng S-box ta được output như sau

Input = 0100 1011 1011 0110

Output = 1101 0011 0011 1000

Shift Row (nibble thứ 2 và thứ 4 hoán vị cho nhau) = 1101 1000 0011 0011

Add Round 2 Key

1101 1000 0011 0011 XOR Key2
= 1101 1000 0011 0011 XOR 1111 0011 0100 1000
= 0010 1011 0111 1011

Vậy ta có ciphertext là:

Ciphertext = 0010 1011 0111 1011

Task 2: Dựa trên kết quả Ciphertext của Task 1, thực hiện giải mã Simplified AES (Decryption) bằng tay để tìm ngược lại Plaintext

Từ Task 1, ta được:

Ciphertext = 0010 1011 0111 1011 Ta sẽ sử dụng cùng các sub-key với các sub-key đã dùng để mã hóa, vì các sub-key này cùng được tạo ra từ cùng một key ban đầu.

Add Round 2 Key

Ciphertext XOR Key2
= 0010 1011 0111 1011 XOR 1111 0011 0100 1000
= 1101 1000 0011 0011

Shift Row = 1101 0011 0011 1000

Inverse Nibble Sub (sử dụng bảng S-box đảo) = 0100 1011 1011 0110

Add Round 1 Key

= 0100 1011 1011 0110 XOR Key1
= 0100 1011 1011 0110 XOR 1111 0000 1011 1011
= 1011 1011 0000 1101

Inverse Mix Columns

S00’ = (9 x 1011) XOR (2 x 1011) = 9 x B XOR 2 x B = C XOR 5 = 1100 XOR 0101 = 1001

S10’ = (2 x 1011) XOR (9 x 1011) = 2 x B XOR 9 x B = 5 XOR C = 0101 XOR 1100 = 1001

S01’ = (9 x 0000) XOR (2 x 1101) = 9 x 0 XOR 2 x D = 0 XOR 9= 0000 XOR 1001 = 1001

S11’ = (2 x 0000) XOR (9 x 1101) = 2 x 0 XOR 9 x D = 0 XOR F = 0000 XOR 1111 = 1111

Ta được output = 1001 1001 1001 1111

Inverse Shift Row = 1001 1111 1001 1001

Inverse Nibble Sub = 0000 1110 0000 0000

Add Round 0 Key =

0000 1110 0000 0000 XOR 0100 1101 0100 1011 = 0100 0011 0100 1011

Vậy,

Plaintext = 0100 0011 0100 1011

Hoàn toàn trùng khớp với

Original = 0100 0011 0100 1011

Việc giải mã được thực hiện xong!